[NOTES/CM-06002] Scattering of Waves

Cross section for waves
The cross section for scattering of waves will now be defined. For the sake of definiteness, let us assume that the incident waves] be electromagnetic wave and the scatter is an electron.

Let the incident waves be plane waves. The scattered waves will be spherical waves moving radially outwards. We define, \[ \text{ Flux }= \text{ Energy transported across unit area per sec},\] the area being perpendicular to the direction of propagation.

We ask how much energy is removed from the beam per sec. Total Energy removed from the incident beam per sec will be proportional to the flux of the incident beam: \begin{equation} \text{Total energy removed from the beam per
sec} =\sigma_t\times \text{Flux},
\end{equation}
or,
\begin{equation}
\sigma_{t}= \frac{\text{Total energy removed from the beam per
sec}}{\text{Incident flux}}
\end{equation}

The differential cross section $\sigma(\theta,\phi)$ is defined by means of the equation.
\begin{equation}
\sigma(\theta,\phi) d\Omega=\frac{\text{ Energy scattered into solid
angle } d\Omega \text{ in direction } \theta,\phi \text{ per
sec}} {\text{Incident Flux}}
\end{equation}
and the total cross section is given by
\begin{eqnarray}
\sigma_t
&=&\int \sigma(\theta,\phi)d\Omega\\
&=&\int_{0}^{2\pi}d\phi\int_{0}^{\pi}d\theta \sigma(\theta,\phi) \sin\theta
\end{eqnarray}

Which area is cross section?
The "cross section" has been defined for waves. What area does does the cross section correspond to? From the definition of cross section we have energy removed from the beam per sec, \begin{equation}\label{EQ14}
=\sigma_t\times \text{ Flux }
\end{equation}
Energy removed from the beam in time $T$
\begin{equation}\label{EQ!5}
=\sigma_t\times \text{Flux} \times T
\end{equation}

Also from the definition of flux, the energy transported across an area $S$ in time \(T\) \begin{equation}\label{EQ15}
= S \times \text{ Flux }\times T
\end{equation}

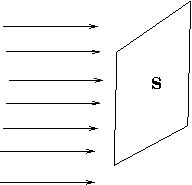
Thus, from \eqref{EQ14} and \eqref{EQ15}, we see that $\sigma_t$ corresponds to the area of the wave front of the incident beam from which energy is removed and scattered. It can, therefore, be said to be the effective area the wave presents to the target. In this view, the cross section has nothing to do with scatterer, the scatterer may even be a point particle.  The cross section for waves should be imagined as an area on the wave front and not of the scatterer.