[NOTES/CM-03004] Applications of Noether's Theorem

 For a system of $N$ particles interacting via potential $V({|\vec x_\alpha}-\vec{x_\beta}|)$ will find symmetries and corresponding conservation laws. \begin{equation}\label{EQ01} L(x,\dot{x})=\frac{1}{2}\sum_\alpha m_\alpha\dot{\vec{x}}_\alpha^{\,2} -\sum_{\alpha<\beta}V(|\vec{x_\alpha}-\vec{x_\beta}|) \end{equation}

Translation symmetry

Consider the translation transformations \begin{equation}\label{EQ02} \vec{x}_\alpha\rightarrow \vec{x}_\alpha^{\,\prime}=\vec{x}_\alpha-\vec{a}. \end{equation} Then we have \begin{equation} \dot{\vec{x}}_\alpha^{\,\prime}=\dot{\vec{x}}_\alpha, \qquad |\vec{x}_\alpha^{\,\prime}- \vec{x}_\beta^{\,\prime}| = |\vec{x}_\alpha-\vec{x}_\beta|. \end{equation}

Translations are a symmetry transformations of the Lagrangian \eqref{EQ01}. To see this consider

\begin{eqnarray}
L(\vec {x}^{\,\prime},\dot{\vec{x}}^{\,\prime})
&=&\frac{1}{2}\sum_\alpha m_\alpha\dot{\vec{x}}_\alpha^{\,\prime2}-
\sum_{\alpha,\beta}
V(|\vec{x}_\alpha^{\,\prime}-\vec{x}_\beta^{\,\prime}|)\\
&=&\frac{1}{2}\sum_\alpha m_\alpha\dot{\vec{x}}_\alpha^{\,\prime2}-
\sum_{\alpha,\beta}V(|\vec {x}_\alpha-\vec{x}_\beta^{\,\prime}|)\\
&=&L(\vec x,\dot{\vec{x}}).
\end{eqnarray}
Therefore, the Lagrangian invariant is invariant under translations.

The constant of motion corresponding to space translations is easily found. The conserved quantities are

\begin{eqnarray}
\sum \frac{\partial{L}}{\partial{\dot q_\alpha}}\delta q_\alpha=\sum
m_\alpha\dot{\vec{x_\alpha}}.\vec a
=\vec a.\sum m_\alpha\dot{\vec{x_\alpha}}
\end{eqnarray}

\begin{equation} \frac{d}{dt}\vec{a}.\vec{p}=0 \Rightarrow \vec{a}.\frac{d}{dt}\vec{p}=0. \end{equation} Since $\vec{a}$ is arbitrary and independent we get the result that conserved quantity corresponding to translations is \begin{equation}\label{EQ09} \frac{d}{dt}\vec p=0.\qquad\qquad \mbox{\text{Prove This.}} \end{equation} where $\vec{p}=\sum_km_\alpha \dot{\vec{x}}_\alpha$ is the total momentum.

Thus we see that invariance under translations gives rise to conservation of total momentum.

For later use, we note that the total momentum is same as \(M\dot {\vec{X}} \), where \(M\) is the total mass and \(\vec{X}\) is the position of the centre of mass. Conservation of total momentum implies that the velocity \(\dot{\vec{X}}\) is constant.

Rotations

Let a set of axes $K^{\,\prime}$ be obtained from a set $K$ by applying rotation about $X_3$ axis by an angle $\theta$ then

\begin{eqnarray}
x^{\,\prime}_{\alpha 1} &=&x_{\alpha 1}\cos\theta + x_{\alpha 2}\sin\theta\\
x^{\,\prime}_{\alpha 2} &=& -x_{\alpha 1}\sin\theta + x_{\alpha 2}\cos\theta\\
x^{\,\prime}_{\alpha 3} &=&x_{\alpha 3}\end{eqnarray}

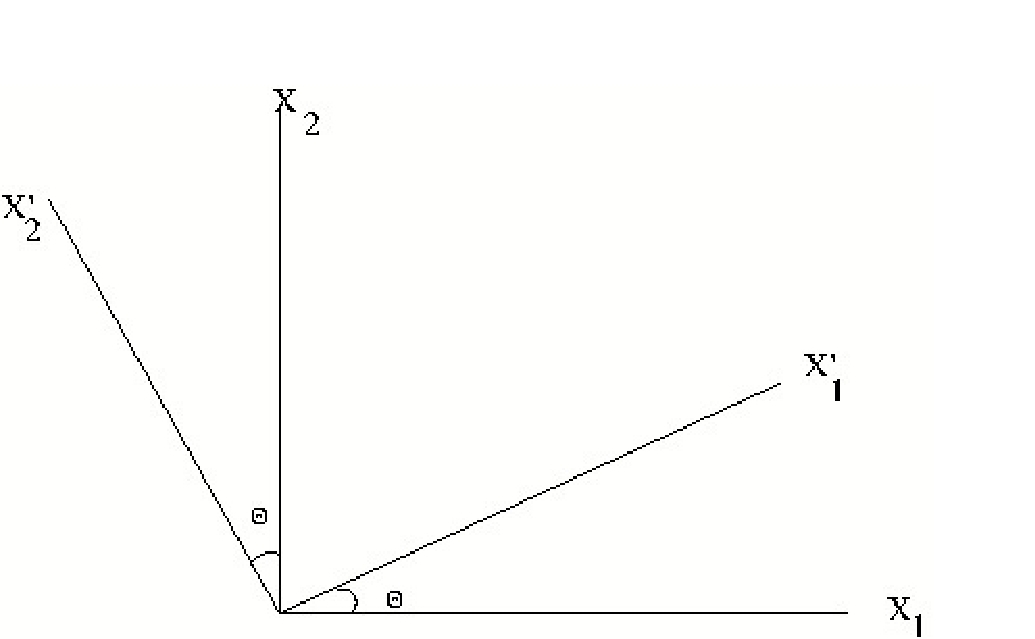
Note that

\begin{eqnarray}

{\dot{x}_{{\alpha 1}}^{\,\prime2}}+{\dot{x}_{{\alpha
2}}^{\,\prime2}} + x_{\alpha3}^{\prime2} 
&=&(\dot{x}_{\alpha 1}\cos\theta+\dot{x}_{\alpha 2} \sin
\theta)^2+(-\dot{x}_{\alpha 1}\sin\theta+\dot{x}_{\alpha 2} \cos
\theta)^2+x_{\alpha3}^{\,2}\\
&=&\dot{x}_{{\alpha 1}}^{\,2}+\dot{x}_{{\alpha2}}^{\,2} +
\dot{x}_{\alpha3}^{\,2}
\end{eqnarray}

Similarly, \begin{equation} {|\vec x_\alpha}^{\,\prime}-\vec{x_\beta}^{\,\prime}|^2={|\vec x_\alpha}-\vec{x_\beta}|^2 \qquad {\dot{\vec{x}}_\alpha^{\,\prime2}}=\vec{x}_\alpha ^2\\ \end{equation}

This implies \begin{equation} L(x^{\,\prime}_\alpha,\dot {x}^{\,\prime}_\alpha)=\frac{1}{2}\sum m_\alpha\dot{\vec{x}}_\alpha^{\,2}+V(|{x_\alpha}-{x_\beta}|)= L(x_\alpha,\dot {x}_\alpha) \end{equation} Therefore, the Lagrangian is invariant under rotations. Let us now compute the variations for small \(\theta\):

\begin{eqnarray}
\delta x^{\,\prime}_{\alpha 1}&=&x_{\alpha 1}\cos\theta+x_{\alpha 2}\sin
\theta-x_{\alpha 1}\\
&\cong& \theta x_{\alpha 2}+O({\theta}^2)\\
\delta x^{\,\prime}_{\alpha 2}&=&-x_{\alpha 1}\sin\theta+x_{\alpha 2}
\cos\theta-x_{\alpha
2}\\
&\cong& -\theta x_{\alpha 1} + O({\theta}^2);\\
\delta x_{\alpha 3}&=&0\\
\end{eqnarray}

Therefore, conserved quantity is

\begin{eqnarray}
G&=&\sum_{\alpha ,k}\frac{\partial{L}}{\partial{\dot {x}_{\alpha,k}}}\delta
x_{\alpha k} \\
&=&\sum_\alpha \Big(\frac{\partial{L}}{\partial{\dot {x}_{\alpha 1}}}\delta
x_{\alpha 1}+\frac{\partial{L}}{\partial{\dot {x}_{\alpha 2}}}\delta x_{\alpha
2}+\frac{\partial{L}}{\partial{\dot {x}_{\alpha 3}}}\delta x_{\alpha 3}\Big)\\
&=&\theta \sum_\alpha\Big(m _\alpha\dot {x}_{\alpha 1}x_{\alpha 2}-m _\alpha\dot
x_{\alpha 2}x_{\alpha 1}\Big)\\
&=&\theta \sum_\alpha m _\alpha\Big(\dot {x}_{\alpha 1}x_{\alpha 2}-\dot
x_{\alpha 2}x_{\alpha 1}\Big)\\
&=&\theta \sum_\alpha\Big(\dot p_{\alpha 1}x_{\alpha 2}-\dot p_{\alpha
2}x_{\alpha 1}\Big) \\
&=&\theta\sum_\alpha\Big(\vec x_\alpha \times \vec p_\alpha \Big)_3
\end{eqnarray}

\begin{equation} \frac{d G}{dt}=0 \Rightarrow \frac{d}{dt}\sum_\alpha\Big(\vec x_\alpha \times \vec p_\alpha \Big)_3=0 \end{equation} Therefore, the third component of angular momentum $L_3=\sum_\alpha\Big(\vec x_\alpha \times \vec p_\alpha \Big)_3 $ is a constant of motion.

Similarly, invariance under rotations about other axes leads to conservation of other components of angular momentum.

Galilean Transformation

The Galilean transformation from a frame to another frame moving with velocity \(\vec{v}\) is given by a frame $$\vec{x}^{\,\prime}=\vec{x}-\vec{v}t$$ where $\vec{v}$ is independent of time. Therefore, $$\dot {\vec x}^{\,\prime}=\dot{\vec{x}}-\vec v$$ and $$ \delta \vec x ^{\,\prime}= -vt;\qquad\delta \dot {\vec x}^{\,\prime}=-v. $$ Since $V(|\vec x_\alpha^{\,\prime}-\vec x_\beta^{\,\prime}|) =V(|\vec x_\alpha-\vec x_\beta|)$, the change in Lagrangian is given by

\begin{eqnarray}
\delta L &=& L(\vec{x}^{\,\prime},\dot{\vec{x}}^{\,\prime})-L(\vec{x},
\dot{\vec{x}})\\
&=&\frac{1}{2}\sum m_\alpha\dot{\vec{x}}_\alpha^{\,\prime\,2}
- \frac{1}{2}\sum m_\alpha\dot{\vec{x}}_\alpha^{\,2}\\
&=&
\frac{1}{2}\sum_\alpha\Big(m_\alpha(\dot{\vec{x}}_\alpha -\vec{v})^2 -
\frac{1}{2}m{\dot{\vec{x_\alpha}}\,^{2}}\Big)\\
&=&-\sum_\alpha (m_\alpha\dot{\vec{x}}_\alpha)\cdot \vec v + O(v^2).
\end{eqnarray}

Thus \begin{equation} L(\vec{x}^{\,\prime},\dot{\vec{x}}^{\,\prime}) = L(\vec x_\alpha,\dot{\vec{ x_\alpha}})-\underbrace{\frac{d}{dt}\sum m_\alpha \vec x_\alpha.\vec v}_{\frac{d}{dt}\Omega} \end{equation} and we have identified \(\Omega\) as indicated above. Therefore, conserved quantity is

\begin{eqnarray}
G&=&\sum_{\alpha, k} \frac{\partial{L}}{\partial{\dot{x}_{\alpha k}}}\delta x_{\alpha k}-\Omega \\
&=&-\sum_{\alpha, k} \dot{x}_{\alpha k} (v_k t) +\sum m_\alpha \vec{x}_\alpha.\vec{v}\\
&=&-\vec{v}\Big(\sum m_\alpha\dot{\vec{x}}_{\alpha}\Big) t-\sum m_\alpha
\vec{x}_\alpha
\end{eqnarray}

Therefore, the quantity $$\vec v\cdot\Big(\sum m_\alpha\dot{\vec x}_{\alpha }\Big) t-\sum m_\alpha \vec x_\alpha$$\\ is independent of time.

To understand the above result a little, let us recall that the definition of the coordinate of centre of mass implies \begin{equation} \sum_\alpha m_\alpha \vec{x}_\alpha= M \vec{X} \qquad \text{and} \quad \sum_\alpha m_\alpha \dot{\vec{x}}_\alpha= M \dot{\vec{X}}. \end{equation} where \(M\) is the total mass of the system. Thus we have $$\vec{v}\cdot\big (\dot{\vec X } t-\vec X\big)= \text{constant}.$$ Since \(\vec{v}\) is arbitrary, we get \begin{equation} \vec{X}= \dot{\vec{X}}t+\text{constant}, \qquad \qquad \HighLight{Write a proof!} \end{equation} Note that at the end of Sec.1, we have already seen that the velocity \(\dot {\vec{X}}\) is constant in time. Therefore $\vec{X}$ is a linear function of time. {\it Thus the conservation law associated with invariance of Galilean transformations is that the centre of mass of the system moves with a constant velocity $\dot{\vec X}.$}