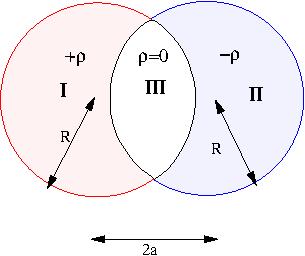
| Problem Two spheres each of radius $R$ are placed so that they partially overlap. The charge densities in the overlap region is zero and in the two non overlapping regions is $+\rho$ and $-\rho$ respectively as shown in figure. The separation between the centers of the spheres is $D$.Find the electric field in the two non-overlap regions. |
 |
Solution
Let the centres of the two spheres be at $\vec{r}_1$ be the position vector of a point in the overlap region drawn from the
center of the first sphere and $\vec{r}_2$ be the position vector of the same point from the center of the second sphere.
The given charge density is equivalent to the two spheres having charge densities \(\pm\rho\) throughout their respective
volumes. Thus the result for a uniformly charged sphere can be applied to the individual spheres
Using superposition principle
- the electric field in the overlap region due to the first sphere = $\displaystyle \frac{\rho \vec{r_1}}{3\varepsilon_0}$
- the electric field due to the second sphere = $\displaystyle - \frac{\rho \vec{r_2}}{3\varepsilon_0}$
Thus the total electric field, using superposition principle,
$$ \vec {E}= \frac{\rho(\vec{r}_1-\vec{r}_2)}{3\varepsilon_0} = \frac{\rho \vec{D}}{3\varepsilon_0}$$
where $\vec{D}=\vec{r}_1-\vec{r_2}$, is the
separation between the centres of the two spheres.
Thus the electric field is constant.






 ||Message]
||Message]
