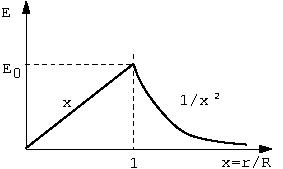
[YMP/EM-02009] Electric Field of a Uniformly Charged Sphere

Let \(\rho\) be the charge density inside a solid sphere of radius \(R\). To find the electric field due to the sphere, we divide the sphere into several thin  shells. Consider one such shell located between \(r\Prime\) and \(r\Prime + d r\Prime\). Then
Volume of this shell \(= 4\pi r{\prime^2}\, dr\Prime\)
Total charge in the shell  \( dq = \rho (4\pi r^{\prime2})\, dr\Prime\). 
The electric field  \(dE\) due to this shell at \(r\) \[ dE= \begin{cases} \frac{dq}{4\pi\epsilon_0 r^{2}} & \text{ if } r> r\Prime\\ 0 & \text{ if } r< r\Prime \end{cases}\]
To get the total electric field, we need to integrate over all shells with radii \(r^\prime\) less than \(r\).

Case I: $r> R$
In this case all thin shells within the sphere contribute to field. Therefore, the electric field at a point outside the sphere is obtained by integrating \(dE\) over \(r\Prime\) from 0 to \(R\) giving
\begin{eqnarray}
 E  &=& \int _0^R \frac{dq}{4\pi\epsilon_0 r^2}
 =\frac{1}{4\pi\epsilon_0 r^2} \int_0^R
 \rho \ 4\pi r^{\prime2} dr\Prime\\
 &=& \frac{1}{4\pi\epsilon_0 r^2}
\frac{\rho\,4\pi R^3}{3}\\
&=& \frac{Q}{4\pi \epsilon_0 r^2}.
\end{eqnarray}
Case II: $r < R$
The contribution of shells with radii greater than \(r\Prime\) vanishes. The contribution at a field point \(r\) to the electric field comes only from shells with radii \(r\Prime < r\). Thus the electric field at a point \(r\) is given by
\begin{eqnarray}
 E  &=& \int _0^r \frac{dq}{4\pi\epsilon_0 r^2}
 =\frac{1}{4\pi\epsilon_0 r^2} \int_0^r
 \rho \ 4\pi r^{\prime2} dr\Prime\\
 &=& \frac{1}{4\pi\epsilon_0 r^2}
\frac{\rho\,4\pi r^3}{3}
=\frac{\rho r}{3 \epsilon_0}.\\
&=& \frac{Q r}{4\pi \epsilon_0 R^3}.
\end{eqnarray}The last step follows using \(Q = \frac{4}{3}\pi R^3 \rho\).
Thus the final expression for the electric field due to a solid sphere of radius \(R\) having total charge \(Q\) is given by \begin{equation} E(r) =\begin{cases} \frac{Q}{4\pi \epsilon_0 r^2}\qquad \text{ if } r> R\\ \frac{Q r}{4\pi \epsilon_0 R^3} \qquad \text{ if } r< R \end{cases}. \end{equation} The field outside the sphere coincides with that of a point charge. Inside the sphere the field is proportional to the distance of the field point from the center. The force felt by  a negative test charge inside the sphere, \(-kr\), coincides with that of a harmonic oscillator.