We will show that the electric field due to a uniformly charged disk at a point on the axis of the disk is given by
|
\begin{eqnarray} At a point on the axis of the disk, only the \(z\) component is non-zero, the other two components vanish, \(E_x=E_y\). |
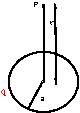 |
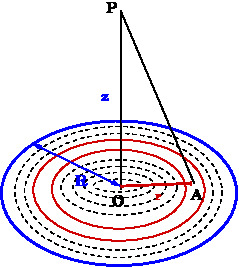
The surface charge density of the disc $\sigma$ is given to be uniform. First divide the disc into several concentric rings and consider one such ring of radius \(r\) and thickness \(dr\). Since the surface charge density is given to be uniform, the only the \(z-\) component of electric field at point \(P\) will be non zero. The area of the ring is \(2\pi r dr\) and hence the charge of this ring is \(dq = 2\pi r\, dr \sigma\). The \(z-\) component of the electric field at point \(P\) can now be written. Thus we have
\begin{eqnarray}
\vec{E}_z=\frac{dq z}{4\pi\epsilon_0(z^2+r^2)^{3/2}} \label{eq10}
\end{eqnarray}
If the radius of the disc is \(a\) and the total charge is \(Q\), we get
\( Q = \sigma (\pi a^2) \Rightarrow \sigma = \frac{Q}{\pi a^2}.\)
Therefore $dq=\sigma (2\pi r dr)=\frac{Q}{\pi a^2}(2\pi r dr) = (2Qr dr)/a^2$. Using the result for the field due to ring we get
 |
\begin{eqnarray} \nonumber\vec{E}_z&=&\frac{2Qz}{a^2 4\pi\epsilon_0}\int_0^a\frac{r dr}{(z^2+r^2)^{3/2}}\\ \nonumber&=&\frac{2Qz}{a^2 4\pi\epsilon_0}\Big[-(z^2+r^2)^{-1/2}\Big]_{r=0}^{r=a}\\ \nonumber&=&\frac{2Qz}{a^2 4\pi\epsilon_0}\Big[-(z^2+a^2)^{-1/2}+\frac{1}{z}\Big]\\ &=&\frac{2Qz}{a^2 4\pi\epsilon_0}\Big[1-\frac{z}{(z^2+a^2)^{1/2}}\Big]\\ \label{eq11} \end{eqnarray} |
For $z>>a$, we use
\begin{equation}
\frac{z}{(z^2+a^2)^{-1/2}} = \big(1+(z/a)^2)^{-1/2}\big) = 1 - \frac{1}{2}\frac{a^2}{z^2} + \ldots,
\end{equation}
in \eqref{eq11} and we get the expected result
\begin{eqnarray}
{E}&\approx&\Big(\frac{2Q}{4\pi\epsilon_0a^2}\Big)\times\frac{a^2}{2z^2}=\frac{Q}{4\pi\epsilon_0z^2} \label{eq12}
\end{eqnarray}
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
