Category:
Relationship between the normal to a surface and the orientation of its boundary curve, as they should appear in Stokes theorem are explained.
The Stokes theorem states that, for a vector field \(\vec F\), we have
$$
\iint\limits_S \vec{\nabla}\times\vec{F}\cdot\overrightarrow{dS} =
\int\limits_\Gamma \vec{F}\cdot\overrightarrow{d\ell}
$$
where $S$ is a surface and $\Gamma$ is the curve forming the boundary of the surface $S$. The normal to the surface \(S\) in Stokes theorem and the orientation of the boundary,\(\Gamma\), of the surface are related. This relationship is explained below with the help of an example of a planar curve \(\Gamma\), shown in figure below.
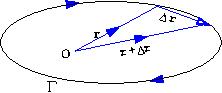 |
Fig 1 A planar curve \(\Gamma\) is shown with two neighbouring points \(P\) and \(Q\). The normal to the area \(S\), enclosed by \(\Gamma\), as given by the cross product \(\vec r\times \overrightarrow{dr}\). In the present example it is to be taken as \(\otimes\), {\it i.e.} into the plane, |






 ||Message]
||Message]
