The method of images makes use of The uniqueness of solutions to boundary value problem makes it possible to relate solution of a given problem in a region \(R\)to another problem with same charge density and boundary conditions. The basic working of the method of images exploits this by for probles involving conductors. It relates the given problem to another problem without conductors but with a set of image charges chosen in a manner that meets the requirement of the uniqueness theorem. The solution to the second problem then provides the desired solution.
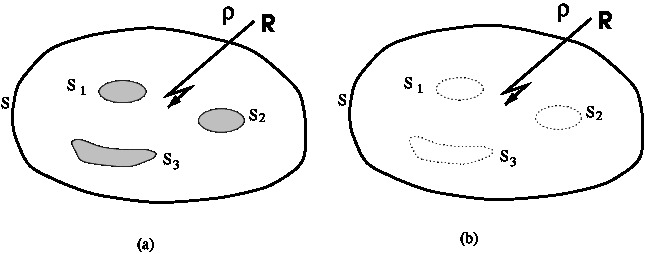
The method of images makes use of uniqueness theorem. Consider a volume \(V\) containing a set of conductors having boundary surfaces \(S_1, S_2, \ldots\) as shown in figure. Let \(S\) be the surface enclosing the volume \(V\). Suppose we are interested in finding the electric potential \(\phi\) in region \(R\) bounded by the surfaces \(S\) and \(S_1, S_2, \ldots\). The electric potential \(\Phi\) in the region of interest is uniquely determined by the charge density in \(R\) and the values of potential on the boundary surfaces \(S, S_1, S_2, \ldots\).
Example
Suppose we want to find the potential \(\Phi\) in region \(R\), which is the volume inside the surface \(S\) and outside the surfaces \(S_1, S_2, S_3\). It is given that
- The region \(R\) has charge density \(\rho\).
- The potential on the boundary \(S\) has a value \(\phi_0\).
- The conductors are held at constant potentials so that potentials on the surfaces \(S_1, S_2, S_3,...\) have values \(\phi_1, \phi_2, \phi_3,...\) respectively.
The uniqueness theorem guarantees that the solution of the above problem coincides with the solution of a second problem differing from the original problem as follows.
- The conductors are removed, only their boundaries are marked.
- Auxiliary charges, called image charges are placed outside region \(R\) in such a manner the potentials on the boundary \(S\) and on the boundaries of the conductors, \(S_1, S_2, S_3,...\) remains as in original problem.
- The only constraint on location of the image charges is that they should be placed outside \(R\). This ensures that the charge density in region of interest remains the same as in the original problem. The desired solution is then given by the potential of the charge distribution \(\rho\) and the image charges.
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
