Category:
In this section the solution of a boundary value problem involving a point charge and a grounded conducting sphere is obtained using the method of images.
Grounded conducting sphere and a point charge
We wish to find potential due to a conducting spherical shell, radius $R$ and centre at the origin \(O\), and a point charge placed at \(A\) \(\vec a, a>R\). The shell is held at zero potential. To solve the problem by the method of images, consider an auxiliary problem shown in \Figref{em-fig-04014}(b), where the conductor has been removed and its boundary is shown by dotted line for reference. We need to find image charge(s) located at distance \(b\), outside the volume of interest \(V\). So we must place the image charge(s) at a distance less than \(R\) from the origin \(O\). The image charge(s) and location(s) must be chosen such that the potential due to the charge on the circle \(\Gamma\) representing the boundary of the shell must add to zero. For considerations of symmetry, the image charge must be placed on the line \(OA\) at some position \(B\).
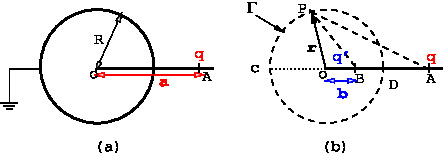
It turns out that one image charge is sufficient. There are two unknowns the value of image charge \(q\Prime\) and distance \(b\) from the origin \(O\). These will be fixed by demanding that that potential, due to the charges \(q, q\Prime\) be zero at the end points \(C,D\) of the diameter \(CD\). This gives the following relations \begin{align}\label{EQ11} \frac{q^\prime}{(R-b)} + \frac{q}{(a-R)} = & 0 \qquad\qquad a>R, \quad b<R\\\label{EQ12} \frac{q^\prime}{(b+R)} + \frac{q}{(R+a)} = & 0 \end{align} These two equations can be solved and give
\begin{equation} \boxed{q^\prime =- \frac{qR}{a} \quad \text{\,and\,}\quad b = -\frac{q^\prime R}{q} = \frac{R^2}{a}} \label{EQ44} \end{equation} Next, we will verify that the potential is zero everywhere on the surface $\Gamma$. Consider a point \(P\) on \(\Gamma\) having position vector \(\vec r\). We know that the potential due to a charge $q$ at position \(\vec a\) and the image charge at \(\vec b\) is \begin{equation}\label{EQ01} \Phi = \frac{1}{4\pi\epsilon_0}\left \{\frac{q}{|\vec{r}-\vec a|} + \frac{q^\prime}{|\vec{r}-\vec b|}\right\} \end{equation} Using \(\hat n\) to denote unit vector along \(OA\), we can write \(\vec a=a \hat n\) and \(\vec b = b \hat n\). We need to check that value of potential, \eqref{EQ01}, at a general point \(P\) at \(\vec r\). We need to verify that the potential be zero every point on the sphere \(\Gamma\). For this purpose, it is sufficient to verify that \begin{equation} q|\vec r- b \hat n| = -q^\prime |\vec r -a\hat n| \end{equation} holds for all directions \(\hat n\). substituting for \(q^\prime\), we see that it is sufficient to verify \begin{equation}\label{EQ02} a |\vec r- b \hat n| = R|\vec r -a\hat n|, \qquad \text{for } |\vec r|=R. \end{equation} for all directions \(\hat n\). So consider square of the left hand side of \eqref{EQ02}
\begin{eqnarray}\nonumber \text{Square of L.H.S. of } \eqref{EQ02} &=& a^2(r^2 + b^2 -2 b(\hat n \cdot \vec r)) \nonumber \\&& \quad \text{Note that} r=R \text{for points on }\Gamma \nonumber\\ &=& (a^2R^2 + a^2b^2 -2b a^2 (\hat n \cdot \vec r ))\\\nonumber &=& R^2(a^2 + R^2 - 2a (\hat n \cdot \vec r))\qquad \because ab=R^2\\ &=& R^2 |\vec r - a\hat n|^2.
\end{eqnarray}
Other related problems
- Point charge near a conducting sphere at a fixed potential. \noindent The conducting sphere at potential $V$ can be replaced by an insulated sphere and a charge $Q=4\pi\epsilon_0RV$ at the origin. This charge produces potential $V$ on the surface of sphere. The final answer for potential outside is given by $$ \Phi = \frac{q}{4\pi\epsilon_0|\vec{r}-\vec{a}|} + \frac{q^\prime}{4\pi\epsilon_0|\vec{r}-\vec{b}|} + \frac{Q}{4\pi\epsilon_0|\vec{r}|} $$ where \begin{align*} q^\prime = & - \frac{qR}{a}\quad,\qquad Q=4\pi\epsilon_0VR\\ \vec{b} = & \hat{n} b\quad, \qquad\qquad b=R^2/a \end{align*}
- Point charge in presence of a charged insulated conducting sphere. This problem is left as an exercise for the reader.






 ||Message]
||Message]
