[NOTES/EM-04007] The Method of Images

 Figure below shows an infinite grounded conducting plane and a point charge located at \((0,0,d)\). The problem is to find the electric potential in region \(R\) in the upper half plane \(\vec r | z >0 \).

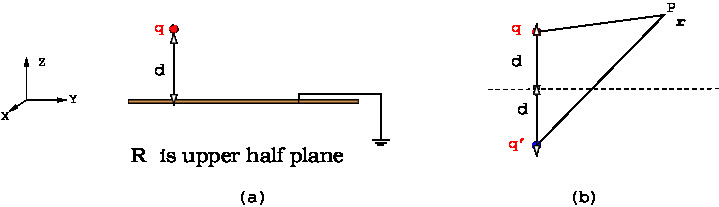
In an auxiliary problem shown in \Figref{em-fig-04015}
Image charge \(-q\) is placed at distance $d$ below the plane. The potential on the plane is zero due to the combined effect of the
charge and image charge. Therefore, by uniqueness theorem,
the electric field, in the region of interest in the arrangement, is equal to
the field due to the given point charge and its image charge. Thus the potential at any point \(P\), position \(\vec r\), is given by
\begin{equation}
 \phi(\vec r)=\frac{1}{4\pi\epsilon_0}\Big(\frac{q}{|\vec r - \vec d|} -\frac{q}{|\vec r + \vec d| }\Big)
\end{equation}
where \(\vec d=(0,0,d)\).
\end{enumerate}