Gauss law is used to determine the electric field near the surface of a conductor is obtained in terms of the surface charge density.
The electric field just outside the surface.
Any net charge on a conductor is distributed on the outer surface. This charge distribution gives rise to electric field just outside the surface. Using Gauss law, we will now show that this field is given by $\dfrac{\sigma}{\epsilon_0}$.
The free charge on a conductor resides on the outer surface. The electric field at every point inside the body of the conductor is zero. Let \(\sigma_P\) denote the surface charge density at a point \(P\) on the surface of the conductor. The electric field near the point \(P\) on surface can be computed using Gauss law.
Let \(\vec E_P\) denote the electric field near the point \(P\). A non zero tangential component of electric field will move the electrons and is not possible in the static situation.
Consider a cylindrical pill box of a small height \(\epsilon\) and bounded by plane surfaces \(S_1\) and \(S_2\). The axis of the pill box is chosen to lie along the normal, \(\hat n\) to the surface at the point \(P\) pointing outward from the conductor.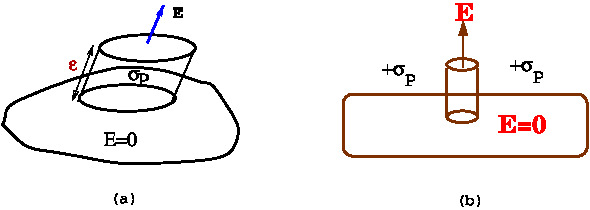
We apply Gauss law to the pill box. If the area of the plane surfaces is \(\Delta S\), applying Gauss law gives
\begin{eqnarray}\label{EQ03}
E_P \Delta S &=& \frac{1}{\epsilon_0}\times \text{Charge enclosed}\\
&=& \sigma_P \Delta S.
\end{eqnarray}
This gives the field near the conductor as
\begin{equation}
\boxed{E_P = \frac{\sigma_P}{\epsilon_0}}
\end{equation}






 ||Message]
||Message]
