[QUE/EM-02024] Electric Field of a Cylindrical Shell

The electric field is to be computed at a point $P$ on the axis of a thin cylindrical shell having uniform surface charge density $\sigma$. Divide the shell by planes perpendicular to the axis, and using the expression for a electric field due to a uniformly charged ring, write expressions for the field as an integral.

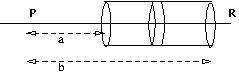
Compute the integral for the cylindrical shell and show that the field due to the cylindrical shell is given by $$ E = \frac{Q}{4\pi\epsilon_0}\frac{1}{(b-a)}\left(\frac{1}{\sqrt{a^2+R^2}}-\frac{1}{\sqrt{ b^2+R^2}}\right) $$ where \(Q\) is the total charge on the cylinder.