[YMP/EM-04004] Grounded Conducting Sphere in Uniform Electric Field

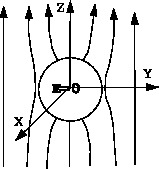
In many boundary value problems, the potential goes to zero at $\infty$. Now we shall solve a problem in which the potential does not go to zero as $\longrightarrow \infty$. \paragraph*{Example} A neutral grounded conducting sphere is kept in a  uniform electric field along the $z$ axis. Find the electrostatic potential every where outside the sphere.

To make use of the spherical symmetry of the problem, we take the center of the sphere as the origin of the coordinate system at the center of the sphere.
Since there are no charges outside the sphere, we solve the Laplace equation for $r>R$. We obtain the solution in four steps.

Step 1  At first we note that the uniform electric field $\vec{E}_0$ corresponds to a potential $\Phi_0$, then
\begin{align}\label{eq001} \vec{E}_0=-\vec{\nabla}\Phi_0\,. \end{align}
The field is given to be along the $z$-axis, so $\vec{E}_0=E_0\vec{k}$. The above equation becomes \begin{align}\label{eq002} - \frac{\partial\Phi_0}{\partial x}\,\vec{i} - \,\frac{\partial\Phi_0}{\partial y}\,\vec{j} -\, \frac{\partial\Phi_0}{\partial z}\,\vec{k} = E_0\vec{k} \end{align} Equation the components, this is equivalent to three equations \begin{align}\label{eq003} \frac{\partial\Phi_0}{\partial x} = 0~;\qquad \frac{\partial\Phi_0}{\partial y}=0~;\qquad \frac{\partial\Phi_0}{\partial x} = -E_0 \end{align} The first two equations show that $\Phi_0$ is independent of $x$ and $y$. Integrating the third equation we get \begin{align}\label{eq004} \Phi_0 = &~-\int E_0dz+C\nonumber\\ =&~-E_0z+C \end{align} In fact the constant $C$ can be set equal to zero without any loss of generality. We shall put $C=0$.

Step 2 The problem has azimuthal symmetry, the potential is independent of the angle $\phi$. The solution of Laplace equation outside the sphere $r>R$ is given by \begin{align}\label{eq005} \Phi(r,\theta) = \sum_{l=0}^\infty\left(A_lr^l+B_lr^{-l-1}\right)P_l(\cos\theta) \end{align} The constant $A_l$ and $B_l$ are to be determined from the boundary conditions as given below.

Step 3 The sphere is grounded hence we must set \begin{align}\label{eq006} \Phi(r,\theta)|_{r=R} = 0 \end{align} for all  \(0\le \theta \le 2\pi\). This gives \begin{align}\label{eq007} \sum_{l=0}^\infty(A_lR^l+B_lR^{-l-1})P_l(\cos\theta)=0 \end{align} Because $P_l(\cos\theta)$ are linearly independent, a linear combination can be zero only if the coefficient of each term is zero. This gives \begin{align}\label{eq008} A_lR^l+B_lR^{-l-1}=0\,,\qquad \text{for all}~~l=0,2,\cdots \end{align} or \begin{align}\label{eq009} B_l=-A_lR^{2l+1} \end{align}

Step 4 At infinity the effect of the sphere should be negligible and the potential $\Phi$ should go to the expression $\Phi_0$. Thus \begin{align}\label{eq010} \lim_{r\to\infty} \Phi(r,\theta) = -E_0z \end{align} At large distance $b_LR^{-L-1}$ term in the potential can be neglected. Imposing the above boundary condition gives \begin{align}\label{eq011} \sum_{l=0}^\infty(A_lr^l)P_l(\cos\theta)= - E_0r\cos\theta \end{align} %Note that $\cos\theta$ is just equal to $P_1(\cos\theta)$. Thus we can rewrite the above equation as \begin{align}\label{eq012} \sum_{l=0}^\infty (A_lr^l)P_l(\cos\theta) = -E_0rP_1(\cos\theta) \end{align} Again we must use the linear independence of the Legendre polynomials. The above equation can hold only if the coefficients of each Legendre polynomial on both sides are equal. This gives \begin{align} A_n = & 0\qquad\qquad\text{for all}~n\ne1 \label{eq013}\\ A_1 = & -E_0\,.\label{eq014} \end{align} Thus all the constant $A_l$ are known. The constants $B_l$ can be solved using the \eqref{eq009}. This gives \begin{align}\label{eq015} B_n=0\qquad\text{for}~n\ne1 \end{align} and \begin{align}\label{eq016} B_1=E_0R^3 \end{align}

Thus only \(n=1\) term remains in the series and all other terms disappear. The solution for the potential becomes. \begin{align}\label{eq017} \Phi_0=-E_0\left(r-\frac{R^3}{r^2}\right)\cos\theta \end{align} The first term correspond to the given uniform electric field. The second term comes from the charges induces on the sphere. The figure below shows the electric field lines for an insulated conductor placed in an external uniform electric field.