[NOTES/EM-10003]-Examples of flow of energy

1.Examples of flow of energy

Consider a volume \(V\) bounded by a closed surface \(S\). The Poynting vector gives the expression for energy flowing into the boundary \(S\) into the volume per unit area per unit time. This total flow per unit time must be equal to the rate of increase of total energy inside the volume.

1.1 Charging of a capacitor

When a capacitor is being charged, the energy stores is increasing with time. Taking an example of a parallel plate capacitor, we will now show that the rate of increase of energy stored is equal to the rate at which the energy flows into the volume between the plates. Rate of increase in energy stored of the capacitor is $\frac{d}{dt}\left(\frac{1}{2}~\frac{q^2}{C}\right) =\frac{q}{C}\left(\frac{dq}{dt}\right)$ \\ We will now compute the flow of energy per sec from the boundary of the capacitor. Note the Poynting vector $$ \vec{N} = \frac{1}{\mu_0}(\vec{E}\times\vec{B}) $$ has a constant magnitude every where on the curved surface $\vec{N}$ and is directed into the volume between the plates.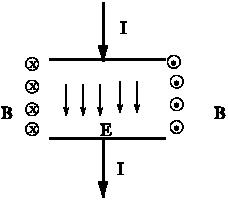{ \begin{align*} E=&\frac{V}{d} = \frac{q}{Cd}\\ B=& \left(\frac{\mu_0}{2\pi a}\right) Id = \frac{\mu_0}{2\pi a} \times (Jd\times\pi a^2)\\ &\hspace{1.75in} \downarrow \text{area of plates}\\ B=&\left(\frac{\mu_0}{2\pi a}\right)\times\left( \frac{\epsilon_0}{Cd}\right) \left(\frac{dq}{dt}\right) \times \pi a^2 \end{align*} }\end{minipage} Therefore, the rate of flow of energy per sec is\\ \begin{align*} \frac{1}{\mu_0}\left|\vec{E}\times\bar{B}\right| \times& \text{curved area} =\frac{1}{\mu_0}\left|\vec{E}\times\vec{B}\right|(2\pi ~ad)\\ =& \frac{1}{\mu_0} E B \times(2\pi ad)\\ =&\frac{1}{\mu_0}\left(\frac{q}{Cd}\right) \times \left(\frac{\mu_0}{2\pi a}\right)\left(\frac{\epsilon_0}{Cd}\right)\left( \frac{dq}{dt}\right) \times\pi a^2\times (2\pi ad)\\ =&\frac{q}{c}\left(\frac{dq}{dt}\right)\left( \frac{\epsilon_0\pi a^2}{Cd}\right)\\ =&\frac{1}{2}~\frac{d}{dt}~\frac{q^2}{C} \end{align*} This shows that the rate of flow of energy into the volume between the plates, as given by the Poynting theorem is equal to the rate of increase of energy of the capacitor.

1.2 Heating of a resistance wire

When a resister is connected to a battery, it gets heated. It will be demonstrated that the heat produced per sec equals the heat flowing in from the boundary as given by the Poynting vector $$ Heat produced per sec =I^2R = \frac{V^2}{R} $$ Let us assume that the resistance wire is of cylindrical shape with radius $a$ and length $L$ and a current $I$ flows into the wire. Due to the current a magnetic field, curling around the wire, will be created as shown.\\ The potential difference between the end points $=V$.\\ This will give rise to electric field $E=V/L$ inside the wire.\\ The direction of Poynting vector $\vec{N}=\frac{1}{\mu_0}(\vec{E}\times\vec{B})$ on the surface is into the volume of the resistance wire. The magnitude of \(\vec{N}\) will be constant all over the curved surface. Value of $\vec{N}=\vec{E}\times\vec{B}$ on the surface of wire has

• magnitude $=EB$
• direction: into the wire

Rate of flow of energy into the wire per sec is \begin{align*} \int_S\vec{N}\cdot \overrightarrow{dS} = & N~\times \text{(curved surface area)}\\ = & N\times 2\pi rL\\ =&\frac{1}{\mu_0}~EB 2\pi rL\\ =& \frac{1}{\mu_0}\left(\frac{V}{L}\right) \times \left(\frac{\mu_0I}{2\pi a}\right)2\pi L a\\ =& IV\\ =& I^2R\quad=\text{Joule heat produced per sec.} \end{align*}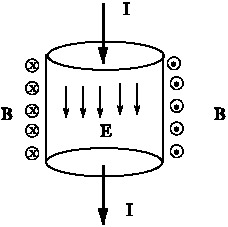

 References 

• Sec 39-6 The Poynting Vector Problems 17, 18 Ch 39 Electromagnetic Waves David Halliday and R. Resnick, Physics Vol-II, Second Edition, (Revised Printing 1966), New Age International Publishers, New Delhi,(1966).