in this section the rule about the direction of cross product the cross product of two vectors is explained.
1.Cross product rule
Vector normal to the plane of paper
We state a convention for direction of vectors perpendicular to the plane of paper. There are two possibilities. A normal vector can be out of the plane, or into the plane of the paper. A circle with a dot. \(\odot\), or dots in a region will be used for the direction out of the plane. A cross \(\otimes\), or into sign \(\times\) will be used to indicate the direction into the plane of the paper. 
Rules for direction of cross product
We require frequent use of vector product $\vec{A}\times\vec{B}$. Let two vectors \(\vec{A}, \vec{B}\) lie in the plane of paper. The rules for the direction of the cross product \(\vec{A}\times\vec{B}\) can be stated in several different ways.
- Draw the vectors $\vec{A},\vec{B}$ (both) away from a point or both towards a point The direction of $\vec{A}\times\vec{B}$ points. out of the paper, \(\textcolor{red}{\odot}\), if rotation from $\vec{A}$ to $\vec{B}$ is anticlockwise.

When clockwise rotation is required to turn $\vec{A}$ to $\vec{B}$ then the direction of $\bar{A}\times\bar{B}$ is into \(\textcolor{red}{\otimes}\) the paper.

It must be remembered that the vectors are drawn in the Figs. \ref{em-cross-07001} and \ref{em-cross-07002} so that both point away from, (or point towards), their meeting point.
- Another way of giving the direction is given in the screen shot, \Figref{em-shot-07001}, of a \href{https://youtu.be/gPnWm-IXoAY?t=159}{youtube video}
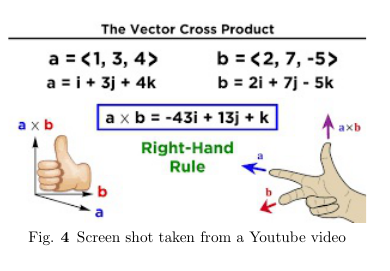 Explanation of right hand rule in \Figref{em-shot-07001} is as follows. Let your fingers point in the direction of the first vector, \(\vec{A}\) and curl around via the smaller angle towards the second vector \(\vec{B}\). Then direction of thumb indicates the direction of the vector product \(\vec{A}\times \vec{B}\). You can find some more popular rules to determine the direction of the cross product. References
Explanation of right hand rule in \Figref{em-shot-07001} is as follows. Let your fingers point in the direction of the first vector, \(\vec{A}\) and curl around via the smaller angle towards the second vector \(\vec{B}\). Then direction of thumb indicates the direction of the vector product \(\vec{A}\times \vec{B}\). You can find some more popular rules to determine the direction of the cross product. References
- Sec. 1.1.1 Vector Operations David Griffiths, Introduction to Electrodynamics, 3rd EEE edn, Prentice Hall of India Pvt Ltd New Delhi, (2002).
- R. P. Feynman, Robert B. Leighton and Mathew Sands Lectures on Physics, vol-II, B.I. Publications (1964)
- YouTube video \url{https://youtu.be/gPnWm-IXoAY?t=159}
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
