Let us look at the motion of a particle under influence of a potential \begin{equation} V(x) = \frac{1}{2}m\omega^2(a x^2-bx^4) \end{equation} We shall be interested in three cases, (i) \(a> 0, b>0\) \ (ii) \(a<0, b>0\) (iii) \(a>0, b<0\).The plot of the potential for the three cases is shown below.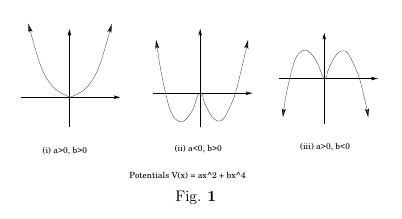
Case(i) $a>0,b>0$ In this case the potential has a minimum at \(x=0\) and goes to infinity as \(x\to \infty\). For any energy \(>0\), there are two turning points and the motion is confined to \(x\) values between the turning points. Thus the motion is bounded and the particle cannot go to infinity.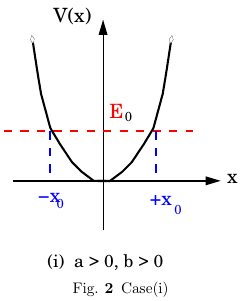
Case (ii) $a< 0, b>0$ In this case the potential is a double well potential with a maximum at \(x=0\) and two minima given by \( x_0 = \sqrt{|a/2b|}\equiv x_0\) at minimum the potential takes value \(V_0=-\frac{a^2}{2b}\).\\ For \( E>0V_\text{min},\text{and} E<0\) the motion is confined between one of the the two regions \(PQ\) or \(RS\) of the \(x\)-axis, see \Figref{3PotsB}. The the initial position of the particle is in the left well, the particle remains confined to \(-x_0 <x<0\). if= the= initial= position= is= in= right= well= it= remains= {\it= i.e.}= will= have= restricted= to= \(rs\).= for= \(e=>0\), there are two turning points and the motion is confined between \(MN\).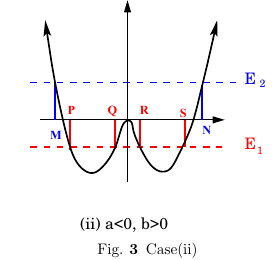
Case (iii) $a> 0, b<0$ In the case the potential has maxima at \(\pm x_0\) and has a double well shape for \(|x|< x_0\) and a minimum at \(x=0\). Outside this range potential monotonically decreases and tends to \(- infty\) as \(x\to \pm \infty\). The points \(x=\pm x_0\) corresponds to an unstable equilibrium. Given a small push, in either direction, it will continue moving in that direction and go to \(\pm\infty\). The points \(x=0\) is a point of stable equilibrium and the particle oscillates about the origin if it has \(E<0\). For example between \(MN\) for \(E=E_0\), see figure 4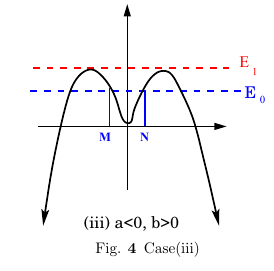
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
