Category:
$\newcommand{\DD}[2][]{\frac{d^2 #1}{d^2 #2}}$
$\newcommand{\matrixelement}[3]{\langle#1|#2|#3\rangle}$
$\newcommand{\PP}[2][]{\frac{\partial^2 #1}{\partial #2^2}}$
$\newcommand{\dd}[2][]{\frac{d#1}{d#2}}$
$\newcommand{\pp}[2][]{\frac{\partial #1}{\partial #2}}$
$\newcommand{\average}[2]{\langle#1|#2|#1\rangle}$
For conservative systems, several statement about the motion of a particle can be inferred from a graph of potential energy, if the value of energy is specified. We explain a set of rules to enable us to use plot of potential energy to get information about general features of motion in one dimension.
Turning Point
As a preparation to the general discussion using plot of potential energy, we explain what is a turning point.
A point \(x\) where the velocity is zero is called a turning point. If \(x_0\) is a turning point, using the energy equation \(E= \frac{1}{2} mv^2 + V(x)\), we see that turning points are obtained by solving the equation \begin{equation}\label{EQ13} E= V(x_0). \end{equation} It is useful to learn how solution of \eqRef{EQ13} can be obtained graphically.
Solving equations graphically:
Solutions of a nonlinear equation \(f(x)=g(x)\) can be obtained graphically. This is done by plotting curves \(y=f(x)\) and \(y=g(x)\) and finding points of intersection, see Figure 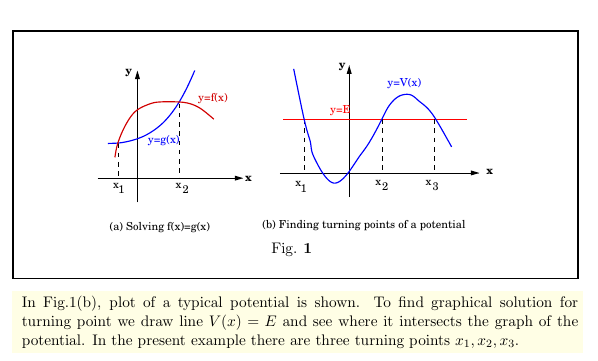 plot of a typical potential is shown. To find graphical solution for turning point we draw line \(V(x)=E\) and see where it intersects the graph of the potential. In the present example there are three turning points \(x_1, x_2, x_3\). }
plot of a typical potential is shown. To find graphical solution for turning point we draw line \(V(x)=E\) and see where it intersects the graph of the potential. In the present example there are three turning points \(x_1, x_2, x_3\). }
1 Qualitative properties of motion in one dimension
We now begin our discussion of general properties of motion in one dimension from the plot of potential energy.
- Since \(E=\) K.E.+ P.E., and kinetic energy is always positive, we must have \(E \ge V(x)\) and the motion is restricted to regions of \(x\) where this inequality is obeyed. Thus a particle cannot go to regions where \(E \le V(x)\). The region of \(x\) where \(E>\text{P.E.}\) is said to be classically accessible.
- At a turning point \(E=V(x)\) and the velocity, \(\dot{x}= \sqrt{\frac{2}{m}(E-V(x))}\), of the particle becomes zero. The subsequent motion of the particle will be in the direction of the force. Remembering that the force is \(F(x)=-\dd[V(x)]{x}\), the force will be in positive \(x\)- direction if the slope is negative. If the slope of potential energy curve is positive the force will be in the negative \(x\)- direction. It is apparent that at a turning point, the particle will move in the direction of decreasing potential.
- At points where the slope is zero, the force is zero and the particle will continue to move in the direction of velocity.
- Let \(x=a\) be a point where the potential is maximum or minimum,then the derivative \(\dd[V(x)]{x}\big|_{x=a}\) vanishes. Thus the force vanishes. If in addition the energy is equal to the potential energy at that point \(V(a)=E\), the velocity of the particle will be zero.\par In this case the particle will be in equilibrium at \(x=a\).
- At a maximum of potential energy a light 'push' will make it move away from the equilibrium point and we say that the maxima of potential energy correspond to points of unstable equilibrium.
- At a minimum of potential energy, a light 'push' will make it move move back towards the equilibrium point and we say that the minima of potential energy correspond to points of stable equilibrium.
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
