[NOTES/ME-02003]-Euler Angles

1. Euler Angles:

The Euler angle parametrization of rotations is very useful in visualization of the solution of the EOM for a rigid body. Let $OX_1,OX_2,OX_3$ (shown in blue) and $OX_1{'},OX_2{'},OX_3{'}$ (shown in red) be two sets of coordinate axes related by a rotation. The orientation of $K{'}$ system relative to $K$ can be completely and uniquely specified in terms of three angles called Euler angles. To define the Euler angles, consider line of intersection of $OX_1,OX_2$ and $X_1{'},X_2{'}$ planes. Let us assume that this line, called the {\it line of nodes}, makes an angle $\phi$ with $OX_1$ and an angle $\psi$ with $X_1{'}$. Let $\theta$ be the angle between the axes $OX_3$ and $OX_3{'}$. The three angles $(\phi,\theta,\psi)$ so defined are called Euler angles.

Fig. 1 : Definition of Euler Angles.

2.Warning:

 Different books use different definitions of the Euler angles. Our definition is the same as that in Goldstein. If the two sets of axes are known, we can obtain the three angles as defined above. Conversely, if the three Euler angles are given, the set $K{'}$ of $X_1{'},X_2{'},X_3{'}$ axes may be obtained as follows by applying three successive rotations.

3 First rotation:

We first rotate the axes in \(K\) the about $X_3$ by angle $\phi$ to get the $\xi_1,\xi_2,\xi_3$ axes, noting that $\xi_3$ will be same as $X_3$ and now $\xi_1$ coincides with the line of nodes. (See figure below.) \paragraph*{Second rotation:} The next rotation is about the line of nodes, {\it i.e.} about $\xi_1$ by angle $\theta$, giving the new axes $\eta_1,\eta_2,\eta_3$. After this rotation $\xi_2$ axis coincides with $\eta_{12}$ and $X_3$ moves to $\eta_3$ which is the final $\equiv X_3'$ axis.

4.Third rotation:

The third and final rotation is about $\eta_3$ by angle $\psi$, giving the axes $X_1{'},X_2{'},X_3{'}$. After this transformation $\eta_3$ axis remains in its position and is identified with $X_3{'}$ axis. The $\eta_1$ moves to $X_1{'}$, $\eta_2$ moves to new position $X_2{'}$.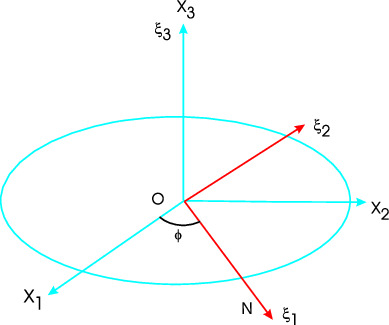

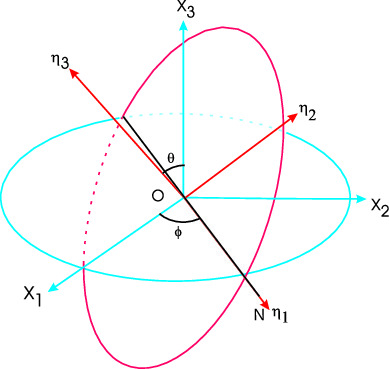
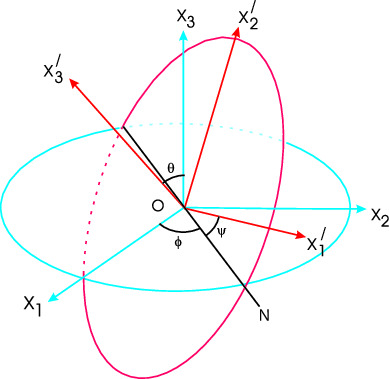
 Fig. 2 : Euler Angles Rotations

The rotation matrix in terms of the Euler angles is \begin{equation} R = R_3(\psi) R_1(\theta) R_3(\phi). \label{EQ63} \end{equation} Here $R_1, R_3$ represent the rotation matrices about the the $x_1$ and $x_3$ axes. Explicitly, we have \begin{eqnarray} R_3(\phi) &=& \left[ \begin{array}{rrr} \cos \phi & \sin\phi & 0 \\ -\sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{array} \right] \\ R_1(\theta) &=& \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \cos \theta & \sin\theta \\ 0 & -\sin\theta & \cos\theta \\ \end{array} \right] \\ R_3(\psi) &=& \left[ \begin{array}{rrr} \cos \psi & \sin\psi & 0 \\ -\sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{array} \right] . \end{eqnarray} The final rotation matrix is given by \begin{equation} R = \left( \begin{array}{ccc} \cos \phi \cos \psi -\cos \theta \sin \phi \sin \psi & \cos \psi \sin \phi +\cos \theta \cos \phi \sin \psi & \sin \theta \sin \psi \\ -\cos \theta \cos \psi \sin \phi -\cos \phi \sin \psi & \cos \theta \cos \phi \cos \psi -\sin \phi \sin \psi & \cos \psi \sin \theta \\ \sin \theta \sin \phi & -\cos \phi \sin \theta & \cos \theta \\ \end{array} \right) \end{equation}