The flux of electric field is defined and As a simple example, the flux of the electric field due to a point charge at the center of a sphere is explicitly computed. Other cases are briefly mentioned an statement of Gauss law is given.
The flux of $\vec{E}$ through a surface, to be denoted by $\Phi$, is defined as a surface integral. The surface is divided into small surface elements \(\Delta S_k, k1,2,\ldots\) and the flux is a limit
\begin{eqnarray} \Phi_S &=&\lim \sum_k\bar{E}_k \Delta\bar{S_k}\cos\theta_k \label{eq2} \\&=&\iint_S(\bar{E}\cdot\hat n){dS} \label{flux-def} \end{eqnarray}
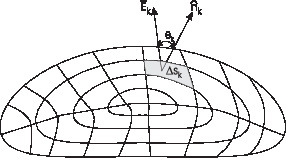
where \(\Delta\bar{S_k}\) is area of the \(k^\text{th}\) element and \(\theta_{k}\) is the angle between normal at the \(k^\text{th}\) area and the electric field at the area element.
Relation of solid angle with flux
The expression for the electric field of a point charge \(q\), located at \(\vec r_0\), \begin{equation} \vec E = \frac{q}{4\pi\epsilon_0} \frac{(\vec r-\vec r_0)}{|\vec r-\vec r_0|^3} \end{equation} shows that the flux of the field of a point charge,\eqref{flux-def}, is proportional to the solid angle, see \eqref{SolidAngle} \begin{equation} \Phi_S\Big|_\text{pt charge} = \frac{q}{4\pi\epsilon_0} \times \text {Solid angle }\Omega_S \end{equation}
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
