Gauss law is applied to compute the electric field for several systems, see the Table of Contents for details. The symmetry of the problem is used in a nontrivial manner to arrive at the answers for the electric field.
In words, the Gauss law states that
the electric flux through any closed surface is proportional to the enclosed electric charge.
Defining flux as $\Phi$, mathematically the Gauss law is;
\begin{eqnarray}
\Phi=\int\bar{E}\cdot dS=\frac{q_\text{enclosed}}{\epsilon_0} \label{eq0}
\end{eqnarray}
We shall now compute $\bar{E}$ in various cases using the Gauss law. This invariably requires the use of symmetry arguments in each case.
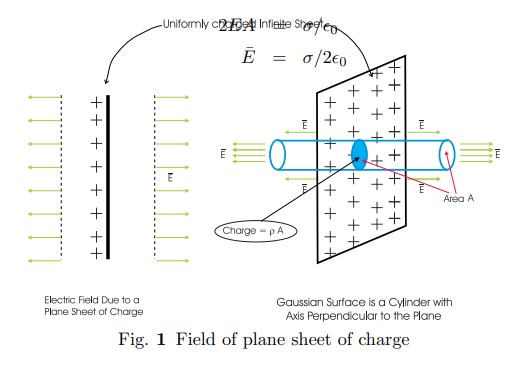
1. Plane sheet of charge
Let the charge density be $\sigma$. To find electric field at a point P ,
consider a gaussian surface which is cylindrical as shown in figure.
Clearly $\bar{E}$ is normal to S and S' Therefor ;
\begin{eqnarray}
\nonumber \text{Flux through S} &=& EA
\nonumber\text{ Flux through S'} &=& EA
\nonumber\text{ Flux through the curved surface} &=& 0
\nonumber \text{Total outward flux} &=& 2EA
\nonumber \text{Charge enclosed} &=& \sigma A
\end{eqnarray}
Therefore using the Gauss law
\begin{eqnarray}
\nonumber 2EA &=& \sigma/\epsilon_0
\bar{E} &=& \sigma/2\epsilon_0 \label{eq1}
\end{eqnarray}
2. Line charge with uniform charge density
Let the charge density be $\lambda$. The field due to line charge at any point P
is perpendicular to the line, the parallel components cancel. This can be
observed by dividing the line charge into 2 small pieces of length dl. Here the
Gaussian surface is a cylinder of radius r and height h passing through P and
the line charges as the axis. $\bar{E}$ is normal to the curved surface and
constant over it.
Therefore the flux through the curved surface $\phi_{cs}$ is
\begin{eqnarray}
\nonumber\phi_{cs}&=& area \mid\bar{E}\mid
&=&\bar{E}\cdot2\pi \bar{r} \times h \label{eq2}
\end{eqnarray}
And the flux through the plane top and bottom surfaces $\phi_{top}$ and
$\phi_{bottom}$ is
\begin{eqnarray}
\nonumber\phi_{top}&=&\phi_{bottom}=0
\end{eqnarray}
This is because the electric field through the two plane surfaces is
perpendicular to the normal $\hat{n}$ at the surfaces and
$\bar{E}\cdot\hat{n}=0$
The total flux $\phi$ is
\begin{eqnarray}
\nonumber\phi &=& \phi_{cs}+\phi_{top}+\phi_{bottom}
&=&\bar{E}\cdot2\pi \bar{r}h \label{eq3}
\end{eqnarray}
Charge enclosed q is
\begin{eqnarray}
q=\lambda h \label{eq4}
\end{eqnarray}
Hence using Gauss law ;
\begin{eqnarray}
\nonumber\bar{E}(2\pi \bar{r})h&=&(\lambda h)/\epsilon_0
\bar{E}&=&\lambda/2\pi\epsilon_0\bar{r} \label{eq5}
\end{eqnarray}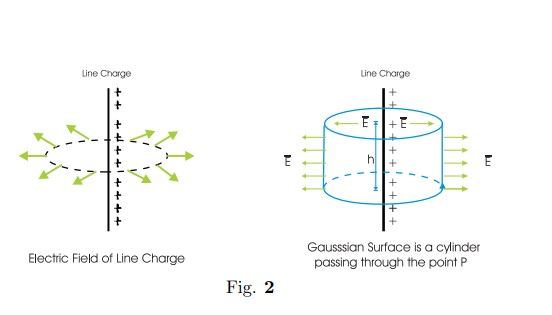
3. Spherical shell with uniform charge density
The electric field $\bar{E}$ is radially outward. The guassian surface is a
sphere of radius.
$\mid\bar{E}\mid$ is constant over the guassian surface and $\bar{E}$ is
parallel to the outward normal $\hat{n}$.
Therefore the flux $\phi$ is ;
\begin{eqnarray}
\nonumber\phi&=&\int\bar{E}\cdot\hat{n}dS
\nonumber&=&\int\mid\bar{E}\mid dS
\nonumber&=&\mid\bar{E}\mid\int dS
&=&\bar{E}4\pi r^2 \label{eq6}
\end{eqnarray}
We know by the Guass law that the charge enclosed is q/$\epsilon_0$
Therefore the electric field of the spherical shell at a distance of r is
\begin{eqnarray}
\bar{E}=q/4\pi\epsilon_0 r^2 \label{eq7}
\end{eqnarray}
For a point inside the shell the guassian surface does not enclose any charge.
Therefore
\begin{eqnarray}
\phi&=&0
\nonumber\bar{E} \times 4\pi r^2& = &0
\bar{E}&=&0 \label{eq8}
\end{eqnarray}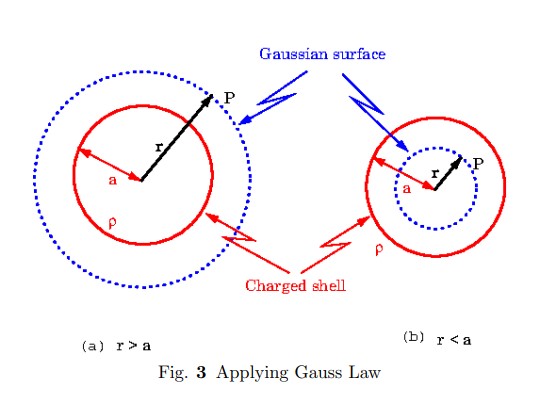
4. Uniformly charged solid sphere
The total charge is q. Guassian surface is a sphere. Charge density of the solid sphere $\rho$ is charge per unit volume.
\begin{eqnarray}
\nonumber\rho&=&q/V
&=&3q/4\pi a^3 \label{eq9}
\end{eqnarray}
Where a is the radius of the gaussian spherical surface from the centre of the solid sphere and r is the radius of the solid sphere.
$a>r$
The point is outside the solid sphere.So the charge enclosed is q. Flux through the guassian surface ;
\begin{eqnarray}
\nonumber\phi&=&\bar{E}\cdot 4\pi r^2 = q/\epsilon_0
\bar{E}=q/4\pi\epsilon_0 r^2 \label{eq10}
\end{eqnarray}
$a< r$
The point is inside the solid sphere. The flux is
\begin{eqnarray}
\phi&=&\bar{E}\cdot 4\pi r^2 \label{eq11}
\end{eqnarray}
Charge enclosed q' is;
\begin{eqnarray}
q'=\rho \frac{4}{3} \pi r^3 \label{eq12}
\end{eqnarray}
Using the Gauss law ;
\begin{eqnarray}
\nonumber\bar{E}\cdot 4\pi r^2&=& \rho \frac{4}{3} \pi r^3/\epsilon_0
\nonumber\bar{E}&=&\rho r/3\epsilon_0
&=&qr/4\pi\epsilon_0 a^3 \label{eq13}
\end{eqnarray}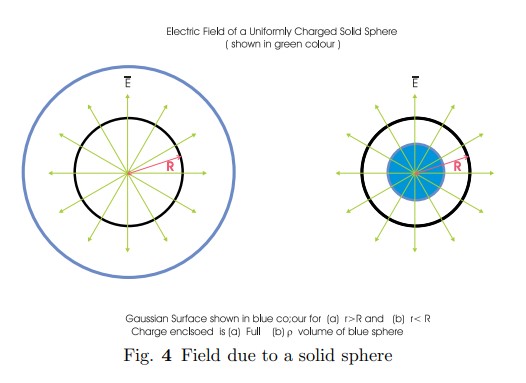
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
