PHY 102: Introduction to Physics-2
Tutorial-9
(Displacement current, Maxwell’s equations and Poynting vector)
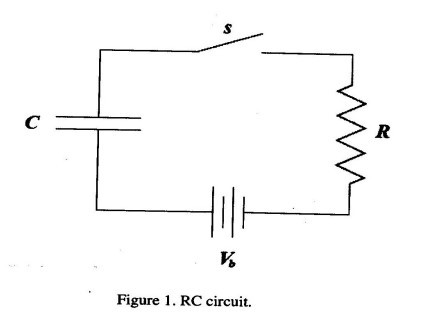
- Displacement current: Consider the following RC circuit (Figure 1). As capacitor $C$ up, a displacement current $I_d$ flows and it induces a magnetic field $B$ inside the plates. Assuming cylindrical plates of radius $a$, calculate $B$ inside the plates.
- Maxwell's equation:
- [(a)]~Use Stoke's theorem to show that the Maxwell equation $\vec{\pmb\nabla}\times\vec{\pmb E}=-{\partial\vec{\pmb B}\over\partial t}$ can be written in the form $$ \oint_C \vec{\pmb E}\cdot d\vec{\pmb l}= - {\partial\over\partial t} \int_S \vec{\pmb B}\cdot d\vec{\pmb S} $$ where the surface $S$ is bounded by the closed curve C.
- [(b)]~Apply the above equation to a loop which straddles the boundary between two materials to show that the tangential component of $\vec{\pmb E}$ must be continuous across the boundary6.
- Poynting vector: A parallel-plate capacitor consists of two circular plates, each with radius $R$ separated by a distance $d$, A steady current $I$ is flowing towards the lower plates and away from the upper plate, charging the plates.
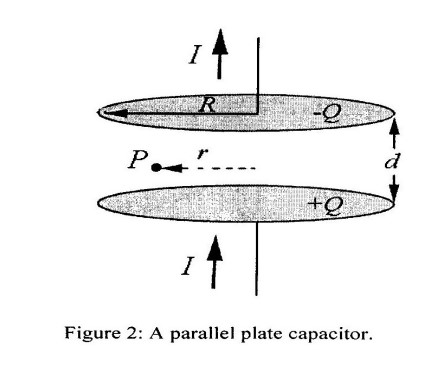
- [a)] What is the direction and magnitude of the electric field $\vec{\pmb E}$ between the plates? You may neglect any fringing fields due to edge effects.
- [b)] What is the total energy stored in the electric field of the capacitor?
- [c)] What is the rate of change of the energy stored in the electric field?
- [d)] What is the magnitude of the magnetic field $\vec{\pmb B}$ at point ${\pmb P}$ located between the plates at radius $r<R$ (see figure above).As seen from above, is the direction of magnetic field clockwise or counterclockwise. explain your answer.
- [e)] Make a sketch of the electric and magnetic field inside the capacitor.
- [f)] What is the direction and magnitude of the Poynting vector $\vec{\pmb S}$ at a distance $r=R$ from the center of the capacitor.
- [g)] By integrating $\vec{\pmb S}$ over an appropriate surface, find the power that flows into the capacitor.
- [h)] How does your answer in part (g) compare to your answer in part (c)?
Exclude node summary :
n
Exclude node links:
0
4727:Diamond Point
0






 ||Message]
||Message]
