[2013EM/HMW-02]

PHY 102: Introduction to Physics-2
Tutorial-2
(Vector calculus)

1. Second Derivative:
   • [(i)] Prove that $\vec{\nabla}\cdot(\vec{U}\times\vec{V})=\vec{V}\cdot(\vec{\nabla}\times\vec{U})-\vec{U}\cdot(\vec{\nabla}\times\vec{V})$.
   • [(ii)] Prove that the curl of a gradient is always zero. Verify it for\\ \(f(x,y,z)=x^2y^2z^4\,.\)
   • [(iii)] Determine the Laplacian of $T=e^{-tx}\sin 4y\cos 3z$.
2. Gauss's theorem: Verify Gauss's divergence theorem for the vector field $\vec{F}=y\hat{i}+2x\hat{j}-z\hat{k}$ and the region $2x+y\le6$, $x\ge 0$, $y\ge0$, $4\ge z\ge0$.
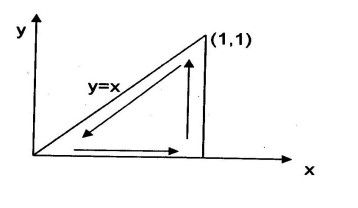
3. Stoke's theorem: An incompressible, steady velocity field is given by: $$ \vec{V} = \left(x^2y-xy^2\right)\hat{i}+\left({y^3\over3}-xy^2\right)\hat{j} $$ For the plane shown below, show that the circulation around the boundary is equal to the surface integral of the curl of the velocity field over the surface (verify Sotkes' Theorem).