Electrodynamics Feb 27, 2019
MID SEMESTER EXAMINATION — Extra Set
-
A gold nucleus contains a positive charge equal to that of 79 protons. An$\alpha$ particle, $Z=2$, has kinetic energy $K$ at points far away from thenucleus and is traveling directly towards the charge, the particle just touchesthe surface of the charge and is reversed in direction. relate $K$ to the radiusof the gold nucleus. Find the numerical value of kinetic energy in MeV is theradius $R$ is given to be $5 \times10^{-15}$ m. \centerline {[ 1 MeV = $10^6$eV and 1 eV = $1.6\times10^{-16}$]
- A line charge carrying a charge \(\lambda\) per unit length and extending from \((-a,0,0)\) to \((+a,0,0)\) lies along the \(x\)- axis. Find the potential at a point on the \(X\)- axis at point \((x,0,0), x>a\) and at a point \((0,y,0)\) on the \(Y\)-axis. Complete the integrations as much as you can.
- Two infinitely conducting coaxial cylinders have radii $a,b$ respectively.
- Compute the electric field between the cylinders.
- Find the electrostatic energy per unit length of the capacitor formed by the cylinders by integrating expression for the energy stored per unit volume of the electric field.
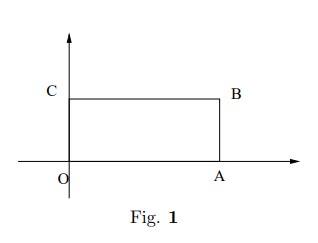
- Solve Laplace equation inside a rectangle \(OABC\) with corners at \((0,0), (a,0), (a,b),(0,b)\) respectively. The sides \(OA\) and \(OB\) are held at zero potential and the sides \(AB\) and \(BC\) are kept at constant potential \(V_0\)
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
