[2019EM/MidSem-1]

                                            Mid Semester Examination∗

B.Sc. IInd                                                                                           Sem MM: 30

1. A circular disk of radius \(R\) carries a surface charge density \(\sigma=kr\). Find the potential at a point on the axis of the disk and distance \(d\) from the center of the disk.
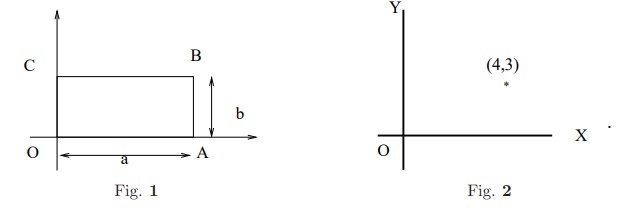
2. Two grounded infinite conducting planes are kept along the \(XZ\) and \(YZ\) planes, see Fig.2. A charge \(Q\) is placed at (4,3) find the force acting on the charge \(Q\). 
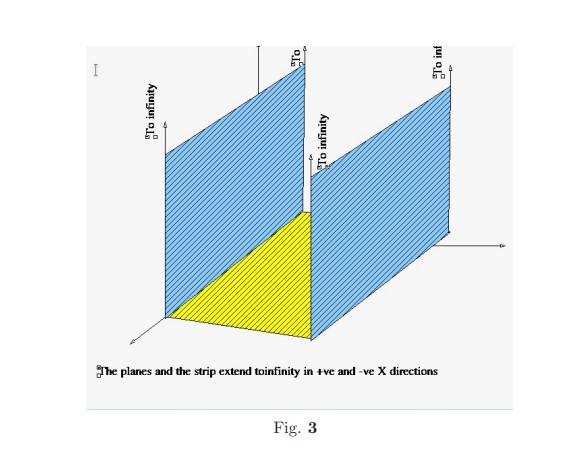
3. Solve the boundary value problem in volume \(V\) bounded by semi-infnite planes (i) Plane 1:\(XZ\) plane extending to infinity in positive \(z\) and both positive and negative \(x\) directions.(ii)Plane 2: Another plane parallel to Plane 1 obtained by translating it to \(y=L\)(iii)Infinite strip: A strip lying in \(XY\) plane between \(0\le y \le L\). The boundary conditions required to be satisfied are \begin{equation} \phi(x,y,z)= \begin{cases} 0 & \text{for } y=0 \text{ and all } x, z\\ 0 &\text{for } y=L \text{ and all } x, z\\ 0 & \text{ as } z \to \infty \\ \cos(3\pi y/L) \sin(5\pi y/L) & \text{ for } z=0 \text{ and } 0\le y \le L \end{cases} \end{equation}