[2019CM/HMW-02]

  Classical Mechanics                              June 1,2009

   Tutorial-II

• For a pendulum with a light rod, as in Fig (a), and pendulum with spring Fig(b), assume that each system can move in all possible ways in space with a fixed point of suspension at the origin. Answer the following questions
  • Write the Lagrangian
  • Identify cyclic coordinates, conserved quantities, if any.
  • Obtain the Lagrangian in small amplitude approximation.
  • Obtain the normal coordinates and normal modes of vibration.
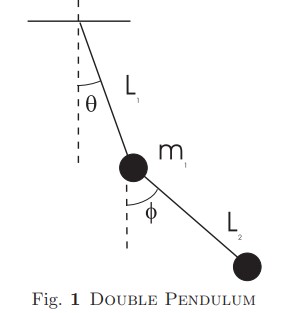
• Set up the Lagrangian for double pendulum consisting of two masses $m_1$ and $m_2$ connected to light bars of lengths $L_1$ and $L_2$ as shown in figure of Double Pendulum.  Use the notation \[ M_2=\mu M_1, L_2=kL_1, g=\nu^2 L_1.\] Obtain the expressions for the following quantities in terms of \(\mu, k ,\nu\).
• • The equation which determines the normal frequencies.
  • Choose \(\mu=\frac{3}{4}, k=\frac{5}{7}\) and find the frequencies of normal modes of vibration.
  • Determine the matrix \(S\) relating the angles to the normal coordinates \begin{equation} \begin{pmatrix} \theta \phi \end{pmatrix} = S \begin{pmatrix}Q_1 Q_2 \end{pmatrix} \end{equation}
  • Verify that the Lagrangian in terms of the normal coordinates takes the form \begin{equation} L = \frac{1}{2}\dot{Q}_1^2 + \frac{1}{2}\dot{Q}_2^2 - \frac{1}{2}\omega_1^2Q_1^2 - \frac{1}{2}\omega_2^2Q_2^2 \end{equation}

• Two systems are shown in {Springs123A}(a) and (b) below.In Fig (a) we have three masses connected to by two springs.The masses can move only along the line joining the three masses.In Fig (b) there are two masses connected by three springs and the system is kept on a smooth horizontal table. One end of each of the two outer springs is tied to fixed nails. The system can can move in all possible ways on the table.

   Set up the Lagrangian and obtain the frequencies of small oscillations.