[2019CM/HMW-01]

                                      Classical Mechanics                              May 23, 2018

                                   

                                              Tutorial-I

1. Set up the Lagrangian for double pendulum consisting of two masses $m_1$ and $m_2$ connected to light bars of lengths $L_1$ and $L_2$ as shown in figure below. 

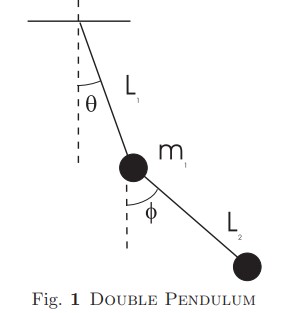
2. A wire is bent in the shape of a parabola \( x^2=4ay\). A bead slides on the wire which is kept in a vertical plane with \(y\)- pointing upwards. How many generalized coordinates are needed? Obtain the Lagrangian and derive the Euler Lagrange equations of motion.Note this problem is slightly different from what is given in the class 

3. A particle moves on the inner surface of a hemispherical bowl of radius \(R\) see Fig below. Choose \(Z\)- axis vertically upwards, \(X,Y\) axes being in the horizontal plane. Using suitable generalized coordinates and set up the Lagrangian of the system.
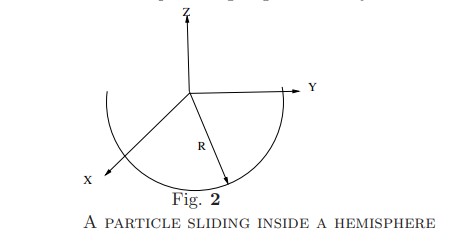
4. A particle moves in two dimensions in potential given by \[ V(x,y)= \frac{\lambda}{r} \] where \(r=\sqrt{x^2+y^2}\). Set up the Lagrangian for the system in parabolic coordinates \(u,v\) defined by \[ x=
6. u^2-v^2, \quad y=2u v.\]
7. Three systems are shown in Fig. (a),(b) and (c). In Fig (a) we have three masses connected to by two springs and free to move in a plane. In Fig (b) there are two masses connected by three springs. One end of each of the two outer springs is tied to fixed nails. The system can oscillate along and perpendicular to the line joining the two masses. In Fig(c) assume that the system can oscillate in vertical direction only. Write the Lagrangian for the three systems