[2019CM/Final-Part-B]

$\newcommand{\Lsc}{\mathscr L}$       

                                                Classical Mechanics                      July 4, 2009                                                                                                                           


End Semester Examination::PART-B

Instruction:-Attempt any four questions. 

1. Consider a particle of mass $m$ moving in two dimensions in a potential The equation of motion for small oscillations are given to be                                                   [4+4+4] \begin{eqnarray} m\ddot{x} =k \big( 5x + y \big)\\ m\ddot{y} =k \big( x + 5 y \big)\nonumber \end{eqnarray}
   1. Find the normal frequencies of vibration of normal modes.
   2. Obtain expressions for \(x,y\) in terms of normal coordinates.
   3. Write the Lagrangian \[{\Lsc} = \frac{m}{2}(\dot{x}^2+m\dot{y}^2) - \frac{k}{2}\big(5x^2+2xy +5y^2\big)\] in terms of normal coordinates and verify that it takes the form \[{\Lsc} = \frac{1}{2}(\dot{Q}_1^2+\dot{Q}_2^2) - \frac{1}{2}(\omega_1^2Q_1^2+\omega_2^2Q_2^2)\]
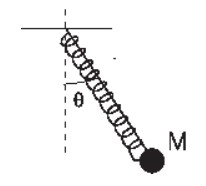
2. Consider pendulum with a spring shown in figure. It oscillates in vertical plane like any simple pendulum.
   1. What is number of degrees of freedom? Which generalized coordinates will you use?[2+2+8]
   2. Write the Lagrangian for the system.
3. A missile is fired from the origin with initial velocity \(u\) and at an angle \(\alpha\) with horizontal.                                                                                               [3+3+3+3] 
1. Write the Lagrangian for the missile.
2. Is there a cyclic coordinate? Which one? What is the conserved quantity associated with it?
3. Is there any other conserved quantity?
4. Using conserved quantities you have found, briefly indicate how a full solution can be obtained.
4. • Show that                                                                                       [3+3+6] \begin{equation*} Q=-p ,\qquad P=q + Ap^2 \end{equation*} (where A is any constant) is a canonical transformation,
     1. [(i)] by evaluating \([Q,P]_{q,p}\)
     2. [(ii)] by expressing \(pdq-PdQ\) as an exact differential \(dF(q,Q)\). Hence find the type one generating function of the transformation. To do this, you must first use the transformation to express \(p,P\) in terms of \(q,Q\).
   • Use the relation \(F_2=F_1+PQ\) to find the type 2 generating function \(F_2(q,P)\),and check your result by showing that \(F_2\) indeed generates the transformation.
5. Consider the motion in a spherically symmetric potential $$ V(r) = - V_0 \left( {3 R\over r } + {R^3\over r^3} \right)$$ If orbital angular momentum of the particle is given by $l^2 = 10 m V_0 R^2$, and answer the following questions.
   1. Plot the effective potential as a function of $r$                                       [3]
   2. What should be the energy of the particle so that it may move in a circular orbit? How many circular orbits are possible? Find the radius of the stable orbit.     [3+3+3]