Category:
$\newcommand{\DD}[2][]{\frac{d^2 #1}{d^2 #2}}\newcommand{\matrixelement}[3]{\langle#1|#2|#3\rangle}\newcommand{\PP}[2][]{\frac{\partial^2 #1}{\partial #2^2}}\newcommand{\dd}[2][]{\frac{d#1}{d#2}}\newcommand{\pp}[2][]{\frac{\partial #1}{\partial #2}} \newcommand{\average}[2]{\langle#1|#2|#1\rangle}
\newcommand{\Label}[1]{\label{#1}}$
Starting from the time dependent Schr\"{o}dinger equation, an equation of continuity \[{\partial\rho\over\partial t} + \vec{\nabla}.\vec{j}=0\] is derived. Physical interpretation of the continuity equation is given in analogy with charge conservation in electromagnetic theory. The equation of continuity represents conservation of probability in quantum mechanics.
We shall discuss some aspects of the Schrodinger equation using the coordinate representation for a particle in a potential $V(\vec{r})$. This will lead us to an interpretation of the wave function, important for scattering problems. The classical Hamiltonian, $H_{cl}$, is \begin{equation} H_{cl} =\frac {\vec{p}\,^{2}} {2 m} +V(\vec{r})\Label{EQ01} \end{equation} The corresponding quantum mechanical operator, $\hat{H}$, in the coordinate representation is obtained by replacement $\vec{p} \to -i\hbar\nabla$ in the classical Hamiltonian. So we have \begin{equation}\Label{EQ02} \hat{H} = -{\hbar^2\over 2m} \nabla\,^2 + V(\vec{r}). \end{equation} The Schrodinger equation assumes the form \begin{equation}\Label{EQ03} i \hbar \frac{\partial\psi(\vec{r},t)}{\partial t} = \hat{H} \psi(\vec{r},t) \end{equation} For motion of a particle in a potential well $V(\vec{r})$, the time dependent Schr\"odinger equation becomes \begin{equation}\Label{EQ05} i\hbar {\partial\psi(\vec{r},t)\over\partial t} = - {\hbar^2\over 2m}{\nabla}^2\psi + V(\vec{r}) \psi(\vec{r},t) \end{equation} Taking complex conjugate we get (assuming the potential to be real $V(\vec{r})^*=V(\vec{r})$ \begin{equation}\Label{EQ06} -i\hbar {\partial\psi^*(\vec{r},t)\over\partial t} = - {\hbar^2\over2m} \vec{\nabla}^2 \psi^*(\vec{r},t) + V(\vec{r})\psi^*(\vec{r},t) \end{equation} If we multiply \eqref{EQ05} by $\psi^*(\vec{r},t)$ and \eqref{EQ06} by $\psi(\vec{r},t)$ and subtract, the potential terms cancel, and we get \begin{eqnarray}\Label{EQ07} i\hbar\psi^*(\vec{r},t){\partial\over\partial t}\psi(\vec{r},t) + i\hbar \psi(\vec{r},t){\partial\over\partial t} \psi^*(\vec{r},t)= -{\hbar^2\over2m}[\psi^*(\vec{r},t)\vec{\nabla}^2\psi(\vec{r},t)-\psi(\vec{r}, t)\vec{\nabla}^2 \psi^*(\vec{r},t)] \end{eqnarray} \eqref{EQ07} can be written as \begin{eqnarray}\Label{EQ08} i\hbar{\partial\over\partial t}\{\psi^*(\vec{r},t)\psi(\vec{r},t)\} = -{\hbar^2\over2m}\vec{\nabla}[\psi^*(\vec{r},t)\vec{\nabla}\psi(\vec{r}, t)-\psi(\vec{r},t) \vec{\nabla}\psi^*(\vec{r},t)] \end{eqnarray} To prove the above the above relation, expand the right hand side of \eqref{EQ08}. It will give four terms, two of which cancel giving the right hand side of \eqref{EQ07}. We define \begin{eqnarray} \Label{EQ09} \rho&=&\psi^*(\vec{r},t)\psi(\vec{r},t)=|\psi(\vec{r},t)|^2\\ \vec{j}&=&-{i\hbar\over2m}\left(\psi^*(\vec{r},t)\vec{\nabla}\psi(\vec{r}, t)-\psi^*(\vec{r},t) \vec{\nabla}\psi(\vec{r},t)\right)\Label{EQ10} .\end{eqnarray}
With $\rho$ and $\vec{j}$ defined as in \eqRef{EQ09} and \eqRef{EQ10}, \eqRef{EQ08} can be written as
\begin{equation}\Label{EQ12} {\partial\rho\over\partial t} +
\vec{\nabla}.\vec{j}=0 \end{equation}
This equation is called the equation of continuity. In electrodynamics a similar relation holds between {\it charge density} $\rho$, and {\it current density} ($\vec{j}$). The equation of continuity represents the law of conservation of charge. Here, in quantum mechanics, $\rho=|\psi|^2$ has the interpretation of probability density. Therefore $\vec{j}$ is called probability current density. As a consequence of \eqref{EQ12}, the total probability $\int_{-\infty}^\infty |\psi|^2d\vec{r}$ is independent of time. To see this, we integrate \eqref{EQ12} over a volume $V$ enclosed by a surface \(S\) to get \begin{eqnarray}\Label{EQ13} {\partial\over\partial t} \int_V \rho d^3x &=& - \int _V \vec{\nabla}.\vec{j}\, dV\nonumber\\ &=& - \int_S (\vec{j}.\hat{n})\, dS \end{eqnarray} where $\hat{n}$ is the unit vector perpendicular to the surface. If $V$ represents volume of a sphere of radius $R$, $S$ will be the surface of the sphere. The surface area increases as $R^2$ when $R$ becomes very large. If $\vec{j}$ decreases faster than $1/R^2$, as $R\to\infty$, the right hand side of \eqref{EQ13} becomes zero when $R\to \infty$. The left side becomes integral over all space and we get \begin{equation}\Label{EQ14} {\partial\over\partial t} {\iiint}_{-\infty}^\infty \rho\, d^3x=0 \end{equation} Therefore the norm \begin{equation}\Label{EQ15} {\iiint}_{-\infty}^\infty \psi^*(x,t)\psi(x,t)\, d^3x=(\psi,\psi)=\|\psi\|^2 \end{equation} is independent of time and \eqref{EQ12} represents conservation of total ``norm'' and is a consequence of the fact $\hat{H}$ is a hermitian operator. The \eqref{EQ14} representing the conservation of total probability follows from \eqref{EQ12}, and \eqref{EQ12} is, in fact, a stronger equation, it represents a local conservation law. The conservation of probability is identical to the equation of continuity for charge conservation in electromagnetic theory. The meaning of different symbols in electromagnetic theory and in quantum mechanics is given in the table below.
| Electrodynamics | Quantum Mechanics | |
| $\rho=$ charge density | Probability density | |
| $\vec{j}=$ (charge) current density | Probability current density | |
| $\int_V\rho d\vec{r}=$ charge in volume $V$ | Probability of finding | |
| particle in volume $V$. | ||
| $\int_S\vec{j}.\hat{n} dS$ current through $S$; | Probability that the particle | |
| charge flowing out of $S$ | crosses the surface in | |
| per unit time | unit time. | |
The physical interpretation of the probability current density can be seen by evaluating it for plane waves \begin{eqnarray} \psi(\vec{r}) &=& N \exp(ipx/\hbar)\nonumber\\ \rho=|N|^2\qquad \vec{j} &=& |N|^2\vec{p}/m = |\bar{N}|^2\vec{v} = \rho \vec{v} \end{eqnarray} The expression (11) for $\vec{j}$ is similar to that for the current density $(\vec{j}=\rho\vec{v})$ in the electromagnetic theory. This expression for $\vec{j}$ can be understood in classical terms if we interpret $\rho$ as number density of particles, then the flux of the beam can be expressed in terms of $\vec{j}$. To see this let us consider a beam of particles incident on a small surface of area $\Delta S$, see Fig.1 below.
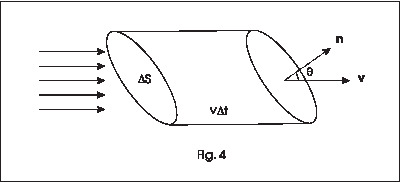 |
| Fig 1. The number of particles crossing \(\Delta S\) per second equals the number in the cylinder |
The number of particles crossing $\Delta S$ in time $\Delta t$ equals the number of particles in a cylinder of height $|\vec{v}|\Delta t $, base $\Delta S$, and having its axis parallel to the velocity $\vec{v}$ of the particles. The volume of the cylinder is given by $\Delta S\cdot\cos\theta(|\vec{v}| \Delta t)$, where $\theta$ is the angle between the velocity $\vec{v}$ and the normal to the surface $\Delta S$. If the number density of the particles is $\rho=|N|^2$,the number of particles in cylinder $=|N|^2\Delta S(\cos\theta) |\vec{v}|\Delta t = \vec{j}\cdot\vec{n} \Delta S \Delta t$. This is the number of particles crossing the surface $\Delta S$ in time $\Delta t$. Thus the flux of particles, defined as the number of particles of the incident crossing a surface per unit area per unit time can be written as $\vec{j}\cdot\vec{n}$ In the above we interpreted $\rho$ as the number density of particles in the beam and concluded that $\vec{j}.\vec{n}$ gives the number of particles crossing a unit area in unit time. For a single particle, $\rho $ has the interpretation of being probability density, and hence $\vec{j}$ will called the probability current density. The current density gives an interpretation of the wave function which has application in scattering problems.






 ||Message]
||Message]
