- Spectral response of an eye $V(\lambda)$ is shown in Fig. 5.1

- Luninous intensity $I$ and illuminance $E$: $$I = \frac{d\Phi}{d\Omega}, E = \frac{d\Phi_{inc}}{dS}.$$
- Illuminance produced by a point isotropic source: $$E=\frac{I\cos(\alpha)}{r^2},$$ where $\alpha$ is the angle between the normal to the surface and the direction to the source.
- Luminosity $M$ and luminance $L$: $$M = \frac{d\Phi_{emit}}{dS}, L=\frac{d\Phi}{d\Omega\.\Delta S \cos(\theta)}
- For a Lambert source $L = const$ and luminosity $$M=\pi L.$$
- Relation between refractive angle $\theta$ of a prism and least deviation angle $\alpha$: $$\sin\frac{\alpha+\theta}{2} = n \sin \frac{\theta}{2},$$ where $n$ is the refractive index of the prism.
- Equation of spherical mirror: $$\frac{1}{s^{\prime}}+\frac{1}{s} = \frac{2}{R},$$ where $R$ is the curvature radius of mirror
- Equations for aligned optical system (Fig. 5.2):
 $$\frac{n^{\prime}}{s^{\prime}}-\frac{n}{s}=\Phi, \frac{f^{\prime}}{s^{\prime}}+\frac{f}{s} = 1, xx^{\prime} = ff^{\prime}$$
$$\frac{n^{\prime}}{s^{\prime}}-\frac{n}{s}=\Phi, \frac{f^{\prime}}{s^{\prime}}+\frac{f}{s} = 1, xx^{\prime} = ff^{\prime}$$ - Relations between focal lengths and optical power: $$f^{\prime} = \frac{n^{\prime}}{\Phi}, f=-\frac{n}{\Phi}, \frac{f^{\prime}}{f} = - \frac{n^{\prime}}{n}$$
- Optical power of a spherical refractive surface: $$\Phi = \frac{n^{\prime}-n}{R}.$$
- Optical power of a thin lens in a refractive index $n_0$: $$\Phi = (n - n_0)\left(\frac{1}{R_1}-\frac{1}{R_2}\right),$$where $n$ is the refractive index of the lens.
- Optical power of a thick lens: $$\Phi = \Phi_1+\Phi_2-\frac{d}{n}\Phi_1\Phi_2,$$where $d$ is the thickness of the lens. This equation is also valid for a system of two thin lenses separated by a medium with refractive index $n$.
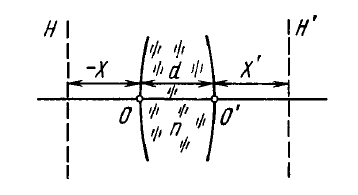
- Principal planes $h$ and $h^{\prime}$ are removed from the crest points $O$ and $O^{\prime}$ of surfaces of a thick lens (Fig 5.3) by the following distances: $$X= \frac{d}{n}\frac{\Phi_2}{\Phi}, X^{\prime}= -\frac{d}{n}\frac{\Phi_1}{\Phi}$$
- Lagrange-Helmholtz invariant: $$nyu = const.$$
- Magnifying power of an optical device: $$\Lambda = \frac{\tan \psi^{\prime}}{\tan\psi},$$ where $\psi^{\prime}$ and $\psi$ are the angles subtended at the eye by an image formed by the optical device and by the corresponding object at a distance for convenient viewing (in the case of a microscope or magnifying glass is equal to $l_0 = 25cm$).
Exclude node summary :
n
Exclude node links:
0
0






 ||Message]
||Message]
