What is the number of irreducible representations of the D-4 group.
Find their dimensions and construct the character table for the group.
You may use the notation and information given below.}
- $\oslash$ Notation for group elements
- Anticlockwise rotation about \(z\)- axis by angle \(\pi/2\) \(:\to 4_z\).
- Anticlockwise rotation about \(z\)- axis by angle \(\pi\)\(:\to 4_z^2\).
- Anticlockwise rotation about \(z\)- axis by angle \(3\pi/2\)\(:\to 4_z^3\).
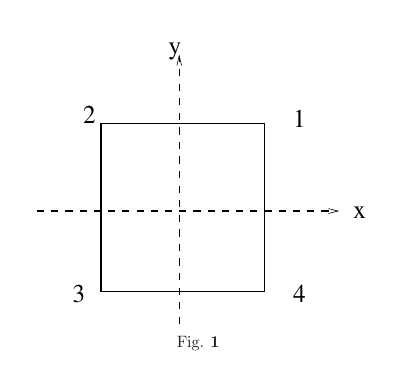
- Reflection in a plane perpendicular to \(X\)- axis \(:\to m_x\)
- Reflection in a plane perpendicular to \(Y\)- axis \(:\to m_y\)
- Reflection in plane containing \(Z\)- axis and diagonal 13 \(:\to m_{13}\)
- Reflection in plane containing \(Z\)- axis and diagonal 24 \(:\to m_{24}\)
The classes are given to be \begin{equation*} \begin{array}{ll} C_1=\{e\}.& \\
C_2 =\{4_z^2\} &C_3 =\{4_z, 4_z^3\} \\
C_4=\{m_x, m_y\} &C_5 =\{m_{13}, m_{24}\}
\end{array}
You may use class multiplication rules \begin{equation*} \begin{array}{llll}
C_2^2=C_1 & C_2C_3=C_3 & C_2C_4=C_4 & C_2C_5 = C_5\\
C_3^2 = 2C_1+C_2 & C_3C_4= 2C_5 & C_3 C_5 = 2C_4 &\\
C_4^2 =2C_1+2C_2 & C_4 C_5= 2C_3 &&\\
C_5^2= 2C_1+2C_2 &&&
\end{array} \end{equation*}
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
