|
|
[QUE/QM-07015]Node id: 2801page$\newcommand{\ket}[1]{|#1\rangle}$
{Let \(\ket{E_1},\ket{E_2}\) denote normalized energy eigenstates with energies \(E_1\ne E_2\). Let \(\psi\) be the superposition \[ \ket{\psi} = a\ket{E_1} + b\ket{E_2},\] \(a,b\) are complex constants. Obtain an expression for the uncertainty in energy \((\Delta E)_\psi\)in the state \(\ket{\psi}\). Find all conditions so that \(\Delta E\) may be zero, and interpret the answers you get.} |

|
22-04-11 13:04:52 |
n |
|
|
[QUE/QM-07014]Node id: 2802page |

|
22-04-11 13:04:13 |
n |
|
|
[QUE/QM-07013]Node id: 2803pageShow that if an operator commutes with to components of angular momentum, it commutes with the third component as well.
{Daniel F. Styer} |

|
22-04-11 13:04:19 |
n |
|
|
[QUE/QM-07012]Node id: 2804page
Consider the space of square integrable functions on a plane. \[ \iint dx\,dy |\psi(x,y)|^2 < \infty.\] Define radial and angular momenta operators \(\hat{p}_r, \hat{P}_\theta\) on the subset of functions satisfying \[\psi(r,\theta+2\pi) = \psi(r,\theta), \qquad \psi(r, \theta)|_{r=0} = \psi(r,\theta)|_{r\to \infty} =0 .\]
- Show that \({P}_{\theta}= -i\hbar\frac{\partial}{\partial\theta}\) satisfies \[\Big(\phi(r,\theta), \hat{P}_\theta \psi(r,\theta)\Big) = \Big(\hat{P}_\theta\phi(r,\theta), \psi(r,\theta)\Big) \] and is, therefore, a hermitian operator.
- Find the hermitian conjugate of the operator \(\hat{p}_r\equiv-i\hbar\frac{\partial}{\partial r}\). Show that \(\hat{p}_r\) is not a hermitian operator.
- Find a hermitian operator \(\hat{P}_r\) that may represent radial momentum in two dimensions.
- Consider the classical free Hamiltonian \( H_{cl} = \frac{P_r^2}{2m} + \frac{P_\theta^2}{2mr^2}.\) Replace the classical momenta \(P_r, P_\theta\) by corresponding hermitian momentum operators \(\hat{P}_r, \hat{P}_\theta\). Compare your answer for the operator so obtained with the free particle Schr\"{o}dinger Hamiltonian \[\widehat{H}_0 = -\frac{\hbar^2}{2m}\Big(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y}\Big).\] and give your comments.
|

|
22-04-11 12:04:28 |
n |
|
|
[QUE/QM-07011]Node id: 2805pageA physical system has dynamical variables $X,Y,Z$ represented by the $2\times2$ Pauli matrices $\sigma_x,\sigma_y,\sigma_z$.
Compute the average value of $\ell X + m Y + n Z $ in any one state in which $a X + b Y + c Z $ has a definite value. Assume $\ell^2 + m^2 +n^2=1$ and $a^2 + b^2 + c^2=1$. |

|
22-04-11 12:04:57 |
n |
|
|
[QUE/QM-07009]Node id: 2807page A physical system has dynamical variables $X,Y,Z$ represented by the
$2\times2$ Pauli matrices $\sigma_x,\sigma_y,\sigma_z$.
Compute the average values of the following operators in the specified
states.
- The average of $X$ in the state represented by the vector $\begin{pmatrix}1 \\ 2\end{pmatrix}.$
- The average value of $Y+Z$ in the state in which the variable $X$ has a definite value -1 for $X$.
|

|
22-04-11 12:04:21 |
n |
|
|
[QUE/QM-07008]Node id: 2808page A physical system has dynamical variables $X,Y,Z$ represented by the $2\times2$ Pauli matrices $\sigma_x,\sigma_y,\sigma_z$.
In each of the following cases find out if the dynamical variables can be measured simultaneously or not.
A physical system has dynamical variables $X,Y,Z$ represented by the $2\times2$ Pauli matrices $\sigma_x,\sigma_y,\sigma_z$. In each of the following cases find out if the dynamical variables can be measured simultaneously or not.
- $X $ and $Y$
- $Y$ and $Z$
- $Y^2$ and $Z$.
|

|
22-04-11 12:04:19 |
n |
|
|
[QUE/QM-07007]Node id: 2809pageA physical system has dynamical variables $X,Y,Z$ represented by the $2\times2$ Pauli matrices $\sigma_x,\sigma_y,\sigma_z$.
Compute the average values and uncertainties of $X,Y$ and $Z $ in a state represented by
$$ \chi = \begin{pmatrix} 1 + 2i \\ 1-3i \end{pmatrix} $$ |

|
22-04-11 12:04:06 |
n |
|
|
[QUE/QM-07006]Node id: 2810pageUse the uncertainty principle to estimate the ground state energy of harmonic oscillator. |

|
22-04-10 18:04:07 |
n |
|
|
[QUE/QM-07001]Node id: 2814pageUse the uncertainty principle to estimate the ground state energy of H- atom. |

|
22-04-10 11:04:52 |
n |
|
|
[QUE/QM-07004]Node id: 2812page Use results of problem [2] to find the minimum value of $V_0$ required to confine an electron inside the nucleus. Take $Z=40$, $ A=64$ and use radius of nucleus $\approx R_0 A^{1/3}$, where $R_0=1.2 \ \mbox{fm} $, to estimate the numerical value of the potential required to confine the electrons inside the nucleus. Compare this with the electrostatic
potential energy of the electron at the surface of the nucleus.
|

|
22-04-10 11:04:53 |
n |
|
|
[QUE/QM-07005]Node id: 2811pageIn the classical kinetic theory of gases, molecules are assumed to be point particles ( of rigid shapes) in motion. Assume the average kinetic energy of the molecules to be ${3\over 2} kT$. Using the uncertainty principle, estimate the minimum uncertainty in position of a molecule. Compare this with average molecular distance for a gas of density $\rho$ ( $\rho=N/V$ , $N=$ number of molecules and $V=$ volume ) When do the quantum mechanical effects become significant ? Estimate this temperature for (a) He gas at normal pressure (b) an electron gas at density of $2.5 \times 10^{22} $ electrons/cc. |

|
22-04-10 11:04:00 |
n |
|
|
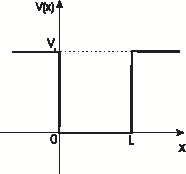
[QUE/QM-07002]Node id: 2815page
Consider a particle in one dimensional square well potential
\begin{equation}
V(x) = \left\{ \begin{array}{ll}
0 & 0 \le x \le L \\
V_0 & \mbox{otherwise}
\end{array} \right.
\end{equation}
For a bound state we should have average energy less than V_0$. $$ \langle E\rangle =\langle T\rangle + \langle V\rangle < V_0 $$
where $\langle T\rangle$ and $\langle V\rangle$ are the averages of the kinetic and the potential energies, respectively. If the article is to be confined to a region of size $L$, use the uncertainty principle to get a rough estimate of average kinetic energy, $\langle T\rangle$. Use this to find approximate minimum value of $V_0a^2$ required for a bound state to exist. |
 |
|

|
22-04-06 16:04:21 |
n |