Category:
We discuss the path independence of the work done by static electric field. This leads to, as in mechanics, introduction of the electric potential. An expression of the electric potential is derived by an explicit computation of work done by on a unit positive charge by the electric field of a point charge \(q\). For an arbitrary distribution of charges, the electric potential is obtained by making use of the superposition principle.
$\newcommand{\mid}{|}$
$\newcommand{\label}[1]{}$
As simple examples of computation of work done, we explicitly compute the line integral $\int_{A}^{B}\vec{E}\cdot\vec{dl} $ for several special paths, here \(A,B\) denote the end points of the path chosen. It will be shown that
\begin{equation} \label{PathInd}
\int_1^2\vec{E}\cdot\vec{dl} =\frac{1}{4\pi\epsilon_0}\Big(\frac{1}{r_1}-\frac{1}{r_2}\Big), \qquad r_1, r_2\ne 0. \end{equation}
where \(\vec{E}\) is the electric field due to a point charge located at the origin \begin{equation} \vec{E} = \frac{1}{4\pi\epsilon_0}\frac{\vec{r}}{r^3}. \end{equation} The distances of points \(A,B\) from the point charge will be denoted by \(r_1, r_2\).
Path I: The curve joining \(A\) to \(B\) is a radial line parallel to the electric field, see Fig. 1. In this case $\vec{E}$ is always parallel to the target at all point on the radial line segment \(AB\), so that \(\vec{E}\cdot\overrightarrow{dl}= E dr\) and
\begin{eqnarray}\nonumber
\int_A^B \vec{E}\cdot\vec{dl} &=&\int_{r_1}^{r_2}\frac{q}{4\pi\epsilon_0r^2}dr =\frac{q}{4\pi\epsilon_0}\Big(\frac{-1}{r}\Big)\Big|_{r_1}^{r_2}\\
&=&\frac{q}{4\pi\epsilon_0}\Big(\frac{1}{r_1}-\frac{1}{r_2}\Big) \label{Eq8} \end{eqnarray}
Path II: Now we take the curve joining points \(A\) and \(B\) to be a circular arc with centre at the origin, therefore \(r_1=r_2\), as shown in Fig. 2. He At each point $\vec{E}$ is perpendicular to the tangent, therefore \(\vec{E}\cdot\overrightarrow{dl}=0\) and we have % \begin{eqnarray} \int_A^B\vec{E}\cdot\vec{dl}&=&0 \label{Eq09} \end{eqnarray}
Path III: Next we compute the line integral giving the work done along a curve consisting a circular arc, \(AC\) and of a radial line \(CB\) and joining two points $A$ and $B$ as shown in Fig. 3
| \begin{eqnarray} \int_{\gamma_1}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_A} - \frac{1}{r_1}\\ \int_{\gamma_2}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_1} - \frac{1}{r_2}\\ \int_{\gamma_3}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_2} - \frac{1}{r_3}\\ \int_{\gamma_4}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_3} - \frac{1}{r_B}. \end{eqnarray} |
|
Work Along a general path
We now give an intuitive argument that the work done by the electric field of point charge located at the origin is given by Eq(1)
An arbitrary path, such as a path \(AA_1A_2A_3B\) shown in Fig 4, can be approximated by paths, \(\gamma_1, \gamma_2, \gamma_3,\gamma_4\) consisting of circular arcs and line segments as in special paths I,I,III discussed above. For these paths the work done by the electric field of a point charge at the origin, is
| \begin{eqnarray} \int_{\gamma_1}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_A} - \frac{1}{r_1}\\ \int_{\gamma_2}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_1} - \frac{1}{r_2}\\ \int_{\gamma_3}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_2} - \frac{1}{r_3}\\ \int_{\gamma_4}\vec E \cdot \overrightarrow{dl} &=& \frac{1}{r_3} - \frac{1}{r_B}. \end{eqnarray} |
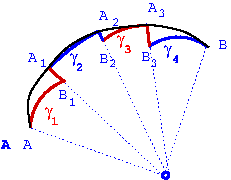 |
The sum of the four contributions to the work
\begin{equation}
\sum_k \int_{\gamma_k}\vec E \cdot \overrightarrow{dl} = \frac{1}{r_A} - \frac{1}{r_B}.
\end{equation}
depends only on the end points \(A,B\). Thus, by making a larger number of subdivisions of the \(AB\), we see that the line integral along the full path remains a function of the end points only. Since this path \(AB\) is arbitrary the path independence of work done by the electric field will hold for all paths.
If the point charge is at $\vec{r_0}$, we would get
\begin{eqnarray}
\int_\gamma\vec{E}\cdot\vec{dl} &=&\frac{q}{4\pi\epsilon_0}\left(\frac{1}{\mid\vec{r}_1-\vec{r}_0\mid} - \frac{1}{\mid\vec{r}_2-\vec{r}_0\mid} \right)
\label{eq15}
\end{eqnarray}
The work done in taking a unit positive charge from a point \(P\) to \(\infty\) is given by charge is
\begin{equation}
\phi(\vec{r}) = \frac{q}{4\pi \epsilon_0}\frac{1}{ \mid\vec{r} -\vec{r}_0\mid}
\end{equation}
This is the potential \(\phi(\vec{r})\) of a point charge \(q\) located at \(\vec{r}_0\).
Therefore, using superposition principle, the potential, at a point \(\vec{r}\), due to several point charges $q_k$, positions $\vec{r}_k$,
is :
\begin{eqnarray}
\phi(\vec{r})&=&\frac{1}{4\pi\epsilon_0}\sum_k\frac{q_k}{\mid\vec{r}-\vec{r}_k\mid
} \label{eq16}
\end{eqnarray}
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]
