[NOTES/EM-02003]-Electric Field due to Continuous Charge Distributions

In the following cases we compute the electric field using Coulumb's law ;

1. Field due to a line charge

The charge per unit length is defined as $\lambda$. Electric field is calculated
at different points P as shown in figures.

Field at an arbitrary point P:

\begin{eqnarray} \vec{E}_x&=&\int\frac{\lambda dx}{4\pi\epsilon_0R^2}(-\sin \theta)\\ \label{eq1} \vec{E}_y&=&\int\frac{\lambda dx}{4\pi\epsilon_0R^2}(\cos\theta) \label{eq2} \end{eqnarray} Integrating the two components using ; $x=dtan\theta$ , $ R=d\sec\theta$ and $dx=d\sec^2\theta d\theta$ \begin{eqnarray} \nonumber\vec{E}_x&=&\int_{\alpha}^{\beta}\frac{\lambda d\sec^2\theta}{4\pi\epsilon_0d^2\sec^2\theta}(-\sin \theta)d\theta\\ \nonumber&=&\frac{\lambda}{4\pi\epsilon_0d} \int_{\alpha}^{\beta}(-\sin \theta)d\theta\\ \vec{E}_x&=&\frac{\lambda}{4\pi\epsilon_0d} (\cos\beta - \cos\alpha)\\ \label{eq3} \vec{E}_y&=&\frac{\lambda}{4\pi\epsilon_0d} (\sin \beta - \sin \alpha) \label{eq4} \end{eqnarray}

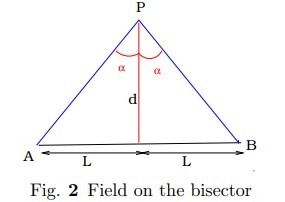
Field at a point at a point on the bisector:

Here $\beta=-\alpha$ and $\sin \alpha=\frac{L}{\sqrt{d^2+d^2}}$ . Therefore \begin{eqnarray} \vec{E}_y&=&\frac{\lambda }{2\pi\epsilon_0d}\frac{L}{\sqrt{d^2+d^2}} \label{eq5}\\ \vec{E}_x&=&0 \label{eq6} \end{eqnarray}

Field due to an infinite line charge

In this case \(\alpha=-\pi/2. \beta=\pi/2\). Therefore the electric field at a distance \(d\) is \begin{equation} E_y = \frac{\lambda}{2\pi\epsilon_0 d}. \end{equation} This agrees with \(L\to \infty\) limit of \eqRef{eq5}

2. Uniformly charged loop

The radius of the loop is $ r_0$. Electric field is calculated at a point on the axis of the loop at a distance z. \begin{eqnarray} \vec{E}_z&=&\int\frac{\lambda dl}{4\pi\epsilon_0 R^2}(\cos\alpha) \label{eq7} \end{eqnarray}

From the figure ; $dl=r_0d\phi$ , $ \cos\alpha=\frac{z}{R}$ and $R=\sqrt{z^2+r_0^2}$\\ \begin{eqnarray} \nonumber\vec{E}_z&=&\int\frac{\lambda r_0 d\phi}{4\pi\epsilon_0 (z^2+r_0^2)}(cos\alpha)=\frac{\lambda z r_0}{4\pi\epsilon_0 (z^2+r_0^2)^{3/2}}\int d\phi\\ \nonumber&=&\frac{\lambda z r_0}{4\pi\epsilon_0 (z^2+r_0^2)^{3/2}}2\pi \\ \vec{E}_z&=&\frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \label{eq8} \end{eqnarray} where $q=2\pi r_0\lambda$ = total charge on the ring.\\ For large z \begin{eqnarray} \vec{E}_z\rightarrow\frac{q}{4\pi\epsilon_0z^2} \label{eq9} \end{eqnarray}

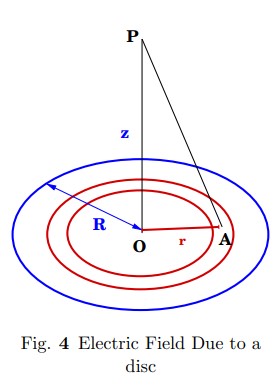
3. Uniformly charged disc

The surface charge density of the disc is defined as $\sigma$. Electric field is $\vec{E}_z$ is defined as the field due to the annular ring between r and r+dr. \begin{eqnarray} \vec{E}_z=\frac{dq z}{4\pi\epsilon_0(z^2+r^2)^{3/2}} \label{eq10} \end{eqnarray} Here ; $dq=\sigma 2\pi r dr=\frac{Q}{\pi a^2}2\pi r dr = \frac{2Q}{a^2}r dr$\\

Therefore \begin{eqnarray} \nonumber\vec{E}_z&=&\frac{2Qz}{a^2 4\pi\epsilon_0}\int_0^a\frac{r dr}{(z^2+r^2)^{3/2}}\\ \nonumber&=&\frac{2Qz}{a^2 4\pi\epsilon_0}[-(z^2+r^2)^{-1/2}]_0^a\\ \nonumber&=&\frac{2Qz}{a^2 4\pi\epsilon_0}[-(z^2+r^2)^{-1/2}+\frac{1}{z}]\\ &=&\frac{2Qz}{a^2 4\pi\epsilon_0}[1-\frac{z}{(z^2+r^2)^{1/2}}]\\ \label{eq11} \end{eqnarray}For $z>>a$ \begin{eqnarray} \nonumber\vec{E}&=&(\frac{2Q}{4\pi\epsilon_0a^2})\frac{a^2}{2z^2}\\ \vec{E}&=&\frac{Q}{4\pi\epsilon_0z^2} \label{eq12} \end{eqnarray}

4. Thin spherical shell

The charge density of the shell is defined as $\sigma$.We know that the field due to a ring for a point on the axis of the ring at a distance \(z\) is ; \begin{eqnarray} \vec{E}_z&=&\frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \label{eq13} \end{eqnarray} Now, we need to compute the electric field due to a thin spherical shell at a point P. Consider a ring shaped slice between planes perpendicular OP at a distance \(x\) and \(dx\) as shown in the figure.This slice is a ring of radius $r_0$lying between angles $\theta$ and $\theta+d\theta$.\\ From the figure, let $x=acos\theta$ , $r_0=acos\theta$ and $z=r-acos\theta$\\

Therefore; \begin{eqnarray} \nonumber r_0^2+z^2&=&a^2\sin ^2\theta + (r-a\cos\theta)^2\\ &=&r^2+a^2-2ar\cos\theta \label{eq14} \end{eqnarray} charge enclosed in the ring of radius $r_0$ \begin{eqnarray} \nonumber q&=&ad\theta 2\pi a \sin \theta \sigma\\ \nonumber&=&\frac{Q}{4\pi a^2}a^2 \sin \theta\, d\theta 2\pi\\ q&=&\frac{Q}{2}a^2 \sin \theta\, d\theta \label{eq15} \end{eqnarray} Therefore electric field along OP at P is; using $t=cos\theta$

\begin{eqnarray} \nonumber\vec{E}&=&\frac{1}{4\pi\epsilon_0}\int_0^{\pi}\frac{Q\sin \theta d\theta(r-a\cos\theta)}{2(r^2+a^2-2arcos\theta)^{3/2}}\\ \nonumber&=&\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1}\frac{dt (r-at)}{2(r^2+a^2-2art)^{3/2}}\\ \nonumber&=&\frac{1}{2}\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1}\frac{1}{r}\frac{ r^2-atr}{(r^2+a^2-2art)^{3/2}}dt \end{eqnarray} \begin{eqnarray} \nonumber&=&\frac{1}{2r}\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1} \frac{r^2+\frac{1}{ 2}(r^2+a^2-2atr)-\frac{1}{2}(r^2+a^2)}{(r^2+a^2-2art)^{3/2}}dt\\ \nonumber&=&\frac{1}{2r}\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1} [\frac{1}{2}\frac{ % % (r^2-a^2)}{(r^2+a^2-2art)^{3/2}}dt+\frac{1}{2} \frac{(dt)}{(r^2+a^2-2art)^{1/2}}] \\ \nonumber&=&\frac{1}{2r}\frac{Q}{4\pi\epsilon_0}[\frac{1}{2}\frac{(r^2-a^2)}{ ar(r^2+a^2-2art)^{3/2}} - \frac{1}{2ar}(r^2+a^2-2art)^{1/2}]_{-1}^{+1} \label{eq16} \end{eqnarray}

Case $r>a$:

\begin{eqnarray} \nonumber\vec{E}&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0}[\frac{(r^2-a^2)}{r-a} - (r-a)- \frac{r^2-a^2}{r+a} + (r+a)]\\ \nonumber&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0}[(r+a) - (r-a)- (r-a)+ (r+a)]\\ &=&\frac{Q}{4\pi\epsilon_0r^2} \label{eq17} \end{eqnarray}

Case $r<a$
\begin{eqnarray} \nonumber\vec{E}&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0}[\frac{(r^2-a^2)}{a-r} - (a-r)- \frac{r^2-a^2}{r+a} + (r+a)]\\ \nonumber&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0}[-(r+a) - (a-r)- (r-a)+ (r+a)]\\ &=&0 \label{eq18} \end{eqnarray}

5. Examples

We will compute the electric field at a points \(P\) and \(Q\) due to charges \(-Q, Q\) at points \(A,B\) respectively as shown in the figure. We will consider the limit when the field points are a much large distance,\(r>>d\), from the charges.
Field due to two charges at \(\pm Q\)}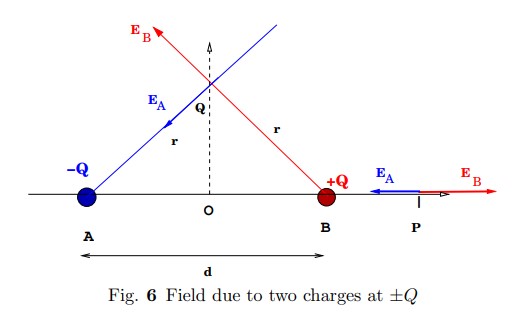

1. Find the electric field at the point \(P\), \(OP=r\), in the figure.

\begin{eqnarray} \nonumber\vec{E}_P&=&\frac{1}{4\pi\epsilon_0}[\frac{q}{(r-d/2)^2}-\frac{q}{ (r+d/2)^2}]\\ \nonumber&=&\frac{q}{4\pi\epsilon_0}[\frac{(r+d/2)^2-(r-d/2)^2}{ (r-d/2)^2(r+d/2)^2}]\\ &=&\frac{q}{4\pi\epsilon_0}\frac{2rd}{(r^2-d^2/4)^2} \label{eq19} \end{eqnarray} When $r>>d$ we get \begin{eqnarray} \vec{E}_P\rightarrow\frac{1}{4\pi\epsilon}\frac{2qd}{r^3} \label{eq20} \end{eqnarray} $\vec{E}_P$ is along the positive \(x\) axis.\\

2. What \(r\) dependence do you expect for a system of charges as shown in the figure?

\begin{eqnarray} \vec{E}_Q=2E\sin \alpha \label{eq21} \end{eqnarray} E= magnitude of $\vec{E}$ due to charge q at Q \begin{eqnarray} E&=&\frac{q}{4\pi\epsilon_0}\frac{1}{r^2+d^2/4}\\ \label{eq22} \nonumber\vec{E}_Q&=&\frac{2q}{4\pi\epsilon_0}\frac{1}{r^2+d^2/4}\frac{d/2}{ (r^2+d^2/4)^{1/2}}\\ &=&\frac{qd}{4\pi\epsilon_0 (r^2+d^2/4)^{3/2}} \label{eq23} \end{eqnarray} Defining $p=qd$ as the dipole moment of the charge system, \begin{eqnarray} \vec{E}_P&=&\frac{p}{4\pi\epsilon_0 (r^2-d^2/4)^{3/2}} \label{eq24} \end{eqnarray} if $r>>d$ \begin{eqnarray} \vec{E}_P&=&\frac{2p}{4\pi\epsilon_0 r^3} \label{eq25} \end{eqnarray} Similarly, \begin{eqnarray} \vec{E}_Q&=&\frac{p}{4\pi\epsilon_0 (r^2+d^2/4)^{3/2}} \label{eq26} \end{eqnarray} if $r>>d$ \begin{eqnarray} \vec{E}_Q&=&\frac{2p}{4\pi\epsilon_0 r^3} \label{eq27} \end{eqnarray}