Category:
The effect of Coriolis force on the force acting on a body on the earth is computed at the poles, equator and at a general point. he banking of railway tracks and of roads is briefly discussed.
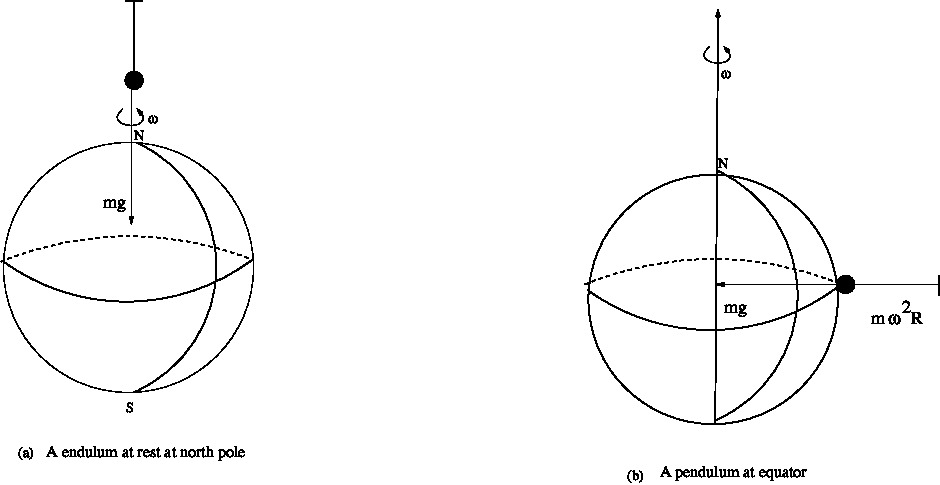
Since the earth is spinning around its own axis, all stationery objects experience centrifugal force on the earth. This causes minute changes in the weight of bodies on the earth. This change varies from point to point on the earth. The centrifugal force is $m \omega^2 R$ where $R$ is the radius of the circle in which the body moves due to earth's rotation. See \Figref{me-fig-061}(a) below. The radius $R$ is $R_0\cos\lambda$, where $\lambda$ is the latitude of the point where the body is located.
North and South Poles:
Consider a body hung with a string at the north pole. Such a body, located at the north or the south pole does not experience any centrifugal force because the radius $R=0$. There is no change in the force of attraction felt by the body towards the centre of the earth.
Equator
The due the attraction of the earth is towards the centre of the earth and the centrifugal (pseudo)force acts in the opposite direction. Thus the force of attraction experienced by the body is $mg-m\omega^2R_0$ and it acts towards the centre. Apparent weight is given by , see \Figref{me-fig-061} \begin{equation} W = mg - m \omega^2 R_0 \label{EQ01}. \end{equation}
Example:The change in weight is maximum at equator and for a body of 10 kg the apparent weight can be computed.(See HCV)
\begin{eqnarray}\nonumber \text{Radius of the earth} R_0= 6400 \text{km} = 64\times 10^5 m\\\nonumber \text{Angular Velocity of the Earth}\\ \nonumber \omega =\frac{2\pi}{24\times60\times60} = 1.82 \text{rad/s} \end{eqnarray}
At Other Points
At any point on the earth, other than the poles and on the equator, the direction of the centrifugal (pseudo)force is not in the same line as the gravitational attraction of the earth. While the gravitational attraction is always towards the centre of the earth, the centrifugal force makes and angle $\frac{\pi}{2} + \lambda$ with the line joining the body and the centre of the earth. See \Figref{me-fig-062}.
The resultant $R$ of the two forces $\vec{P},\vec{Q}$ making an angle $\alpha$ is is given by the formula
\begin{eqnarray} R^2 = P^2 + Q^2 + 2 PQ \cos\alpha \label{EQ02}\\ \tan \theta = \frac{Q\sin\alpha}{P+Q\cos\alpha} \label{EQ03} \end{eqnarray}
where $R$ is the magnitude of the resultant force $\vec{R}$ and $\theta$ is the angle that $\vec{R}$ makes with $\vec{P}$.
In our case \begin{eqnarray} P = mg; \qquad Q =m\omega^2 R; \quad \alpha = \frac{\pi}{2}+\lambda \label{EQ03A} \end{eqnarray}
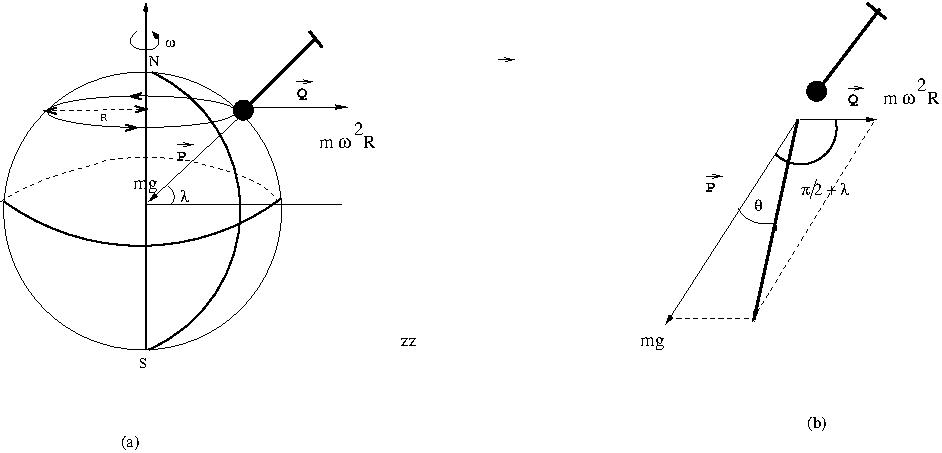 |
| Fig 1.(a) Directions of earth's attraction and centrifugal forces on the surface of the earth (b) Rule for vector addition of two forces |
Therefore the apparent weight which is the vector sum of the earth's attraction and the centrifugal force is given by
\begin{eqnarray} W &=& m\sqrt{g^2 +(\omega^2R\sin\lambda)^2 -2 g(\omega^2R\sin\lambda) }\\ \tan \theta &=& \frac{\omega^2R\sin\lambda}{g+\omega^2R\sin\lambda},\qquad \cos\alpha = -\sin\lambda\\ \end{eqnarray}
where $\theta$ is the angle that a suspended body makes with the true vertical, {\it i.e} with the radius vector drawn from the centre of the earth.
Banking of Railway Tracks and Roads
For a train taking a turn, while moving on a circular track, the centripetal force is provided by the reaction of the railway lines. The magnitude of the reaction needed is $mv^2/R$. For a fast moving trains and also for a sharp turns will experience to outward centrifugal horizontal force. With only elastic forces due to the track to balance this outward horizontal force in normal course, this will cause a strain in the tracks and for large speeds and sharp curves the railway lines may get damaged. In such a case the train will jump off the tracks. This is avoided by banking of the railway tracks near sharp turns.
The curved part of the railway track not kept in a horizontal plane it is tilted towards the centre of the circular arc for the required movement of the train. The normal reaction due to railway line will then have a vertical and a horizontal components. With suitable banking the centrifugal force and the horizontal components will nearly balance, leaving a much smaller stress on the railway line.
Essentially the same thing works for banking of the roads near a sharp turn. Without banking of the road, frictional forces will provide suitable centripetal force required for turning a vehicle. Since there a limit to maximum possible value of the frictional force, beyond certain speeds and for sharp curves the vehicle will skid and banking of the road is a must for smooth driving.






 ||Message]
||Message]
