[2013EM/HMW-05]

PHY 102: Introduction to Physics-2
Tutorial-5
(Electric field, electric potential, energy in electrostatic field)

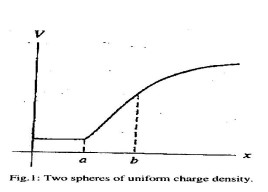
1. Sketch the electric field:  Figure 1 shows the potential of a charge distribution as a function of $x$. Sketch a graph of the electric field $E_x$ over the region shown.
2. Electric potential and electric field lines: The potential in a certain region is given by $V=axy$, where $a$ is a constant. (a) Determine the electric field in the region. (b) Sketch some equipotentials and field lines.
3. Energy stored in a continuous charge distribution: Find the energy stored in a uniformly charged solid sphere of radius $R$ and total charge $q$ using three different equations as follows:
   1. [(a)] $W={1\over2}\int \rho V~d\tau\,$.
   2. [(b)] $W= {\epsilon_0\over2}\left[\int_{\rm Surface} V\vec{E}\cdot d\vec{a}+\int_{\rm Volume} E^2 d\tau\right]$
   3. [(c)] $W={\epsilon_0\over2}\int_{\rm all~surface} E^2d\tau$.

   \begin{align*}E =& {\rho r\over 3\epsilon_0} \qquad\qquad r<R,\qquad\qquad\text{inside ~a~ sphere}\\=&{\rho\times {4\over3}\pi R^3\over 4\pi\epsilon_0 r^2} = {\rho R^3\over 3\epsilon_0r^2}\qquad\qquad \text{outside~sphere}\end{align*}