Consider a closed cylinder whose walls are adiabatic. The cylinder is divided into three equal parts $A_1$, $A_2$ and $A_3$ by means of partitions $S_1$ and $S_2$, which can move along the length of the cylinder without friction. The partition $S_1$ is adiabatic and $S_2$ is conducting. Initially, each of the three parts contain one mole of Helium gas, which can be treated as an ideal gas, is at pressure $P_0$, temperature $T_0$ and volume $V_0$. Assume the specific heat at constant volume $C_v\,=\,\frac{3R}{2}$ and the specific heat at constant pressure $C_p\,=\,\frac{5R}{2}$. Now, heat is supplied to the to the left most partition $A_1$ till the temperature in part $A_3$ becomes $T_3\,=\,\frac{9T_0}{4}$ Find the final volume, pressure and temperature in terms of $V_0$, $P_0$ and $T_0$. Assume the entire process is quasistatic.
\vskip 3mm
3. ( Continuation of problem 2)
(a) What is work done by the gas in $A_1$ ?
(b) What is the heat supplied to the gas in $A_1$?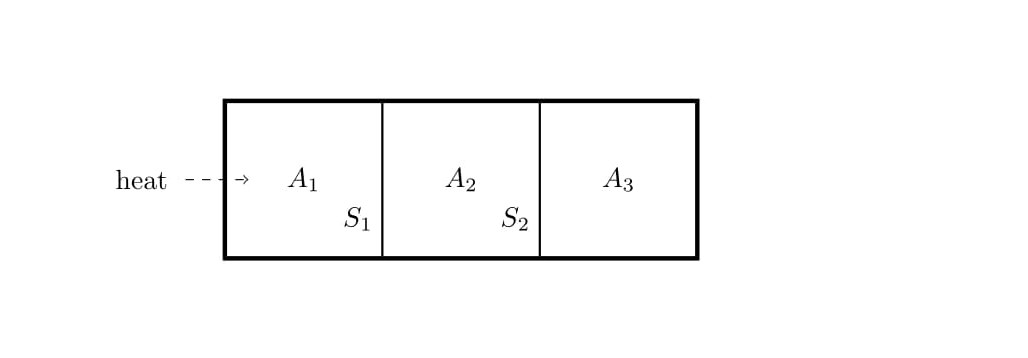
Exclude node summary :
Exclude node links:
5017:TH-HOME,4727:Diamond Point






 ||Message]
||Message]
