Thermal Physics
Problem sheet 5
Each question carries 5 marks
19th October 2021
Due 26th October 2021
Reading Assignment : See attachment about rubber band
13.CD consists of two adiabatic processes and an isobaric process and an isochoric process of a box of volume V containg perfect gas as shown below 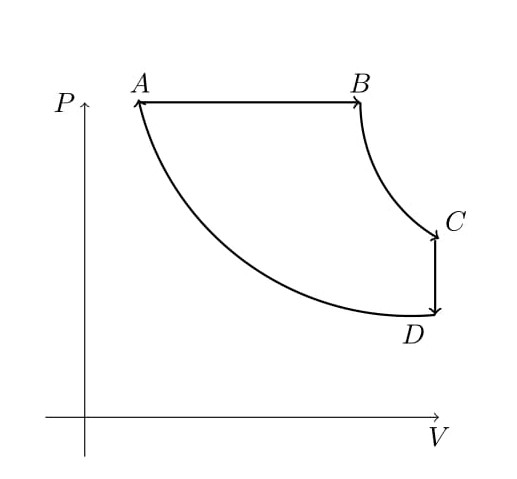
AB is constant volume BC and DA and adiabatic and CD is at constant volume. Calculate the efficiency of the engine in terms of $V_A$, $V_B$, $V_C$ and the ratio of specific heats $\gamma$. Remark : The efficency depends upon the equation of state of the system. had we used some other system ( like a gas of photons, whose equation of state, we will discuss soon) the answer is different). Only for carnot's cycle, the efficency is independent of the system.)
14. Let $$\frac{\partial (x,y)}{\partial (a,b)}\,\equiv\,\left|\begin{array}{ll} \frac{\partial x}{\partial a}&\frac{\partial y}{\partial a}\\ \frac{\partial x}{\partial b}&\frac{\partial y}{\partial b}\\ \end{array}\right|$$ Then show that $$ \frac{\partial (x,y)}{\partial (a,b)}\frac{\partial (a,b)}{\partial (c,d)}\,=\,\frac{\partial (x,y)}{\partial (c,d)} $$
Remarks :
1. This can be generalised to higher dimensions.
2. This can be found in books - and is very useful in changing variables in multiple integrals.
15. Show that if $$ \left(\frac{\partial U}{\partial V}\right)_T\,=\,0$$ then $$ \left(\frac{\partial U}{\partial P}\right)_T\,=\,0 $$ with $$ \left(\frac{\partial P}{\partial V}\right)_T\,\neq\,0$$
10 The tension $\tau$ in an elastic rubber band is given by $$ \tau\,=\,aT\left(\frac{L}{L_0(T)}-\,\left(\frac{L_0(T)}{L}\right)^2\right),$$ where $a$ is a constant, $L_0(T)$is the unstretched length at zero tension, and is a function of temperature only.
(a) Write the first law using the work done when it is elongated and gets a supply of heat. ( Be careful of signs!)
(b) Use the first law to write $dF$, where $F$ is the free energy of the rubber band.
(c) Solve for the free energy $F$ and show that $$ F(T,L)\,-\,F(T,L_0(T))\,=\,aT\left(\frac{L^2}{2L_0(T)}\,+\,\frac{L_0(T)^2}{L^2}\,-\,\frac{3L_0(T)}{2}\right)$$ and the entropy $S$ $$ S(T,L)\,-\,S(T,L_0(T))\,=\,a\left(\frac{3L_0}{2}\,-\,\frac{L_0^2}{L}\,-\,\frac{L^2}{2L_0}\right)\,-\,aT\left(\frac{3}{2}\,-\,\frac{2L_0}{L}\,+\,\frac{L^2}{2L_0^2}\right)\frac{dL_0(T)}{dT} $$
11. ( refer to the previous problem.)
(a) Find the heat $Q$ transferred to the elastic band when it is stretched from $L_0$ to $L$ isothermally.
(b) Show that $$ \left(\frac{\partial T}{\partial L}\right)_S \,=\,\frac{aTL_0^2}{c_LL^2}\left(-1\,+\,\left(\frac{L}{L_0}\right)^3\,+\,\frac{Ta}{L_0}\frac{dL_0}{dT}\left(2\,+\,\left(\frac{L}{L_0}\right)^3\right)\right)$$ where $$c_L\,=\,\left(\frac{DQ}{\partial T}\right)_L.$$
12. Consider a cycle $ABCD$ with perfect gas as the working substance. $AB$ is at constant volume $V_1$ and $CD$ is at constant volume at $V_2$ with $V_2\,>\,V_1$ The parts $BC$ and $DA$ are adiabatic. Calculate the efficiency of this engine in terms of $V_!$ and $V_2$. (Note this is different from Carnot's engine and so we can not draw similar conclusions about the efficiency being maximum) Find $B$ and $n$.
21Th-ProbSet5
For page specific messages
For page author info
n
0






 ||Message]
||Message]
